A Tradeoff Between Accuracy and Flexibility in a Working Memory Circuit Endowed with Slow Feedback Mechanisms

Abstract

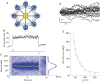
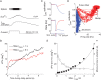
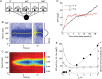
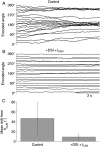
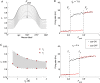
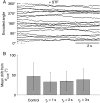
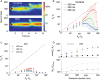
Recent studies have shown that reverberation underlying mnemonic persistent activity must be slow, to ensure the stability of a working memory system and to give rise to long neural transients capable of accumulation of information over time. Is the slower the underlying process, the better? To address this question, we investigated 3 slow biophysical mechanisms that are activity-dependent and prominently present in the prefrontal cortex: Depolarization-induced suppression of inhibition (DSI), calcium-dependent nonspecific cationic current (ICAN), and short-term facilitation. Using a spiking network model for spatial working memory, we found that these processes enhance the memory accuracy by counteracting noise-induced drifts, heterogeneity-induced biases, and distractors. Furthermore, the incorporation of DSI and ICAN enlarges the range of network's parameter values required for working memory function. However, when a progressively slower process dominates the network, it becomes increasingly more difficult to erase a memory trace. We demonstrate this accuracy-flexibility tradeoff quantitatively and interpret it using a state-space analysis. Our results supports the scenario where N-methyl-d-aspartate receptor-dependent recurrent excitation is the workhorse for the maintenance of persistent activity, whereas slow synaptic or cellular processes contribute to the robustness of mnemonic function in a tradeoff that potentially can be adjusted according to behavioral demands.

Keywords: DSI; ICAN; persistent activity; prefrontal cortex; synaptic plasticity.

Figure 1.

Persistent activity and random drifts of a memory trace in a spiking network model for spatial working memory. (A) Schematic of the network connectivity (all-to-all) between the excitatory (blue circles) and inhibitory (yellow circle) neurons. Light gray and black connectors indicate, respectively, excitatory and inhibitory synapses. Each excitatory cell is selective for a direction (black arrows), and the strength of connection between 2 excitatory cells is a decreasing function of the difference in their preferred directions. (B) Lower panel: applied current to excitatory cells. The first positive step current corresponds to cue presentation. The second negative current represents a shutdown signal. Upper panel: average firing rate of a group of 200 neurons (with preferred directions around cue location) during a trial. The activity ramps up during cue presentation, persists during delay, and is reset to a spontaneous baseline by the shutdown pulse. (C) Left panel: spatiotemporal pattern of excitatory cells of the same simulation as in (A) (cue presented at 180°). Each dot represents a spike. The yellow line is the population vector, which traces the peak of the bell-shaped persistent activity pattern (bump attractor) as the internal representation of the cue location. Right panel: Population firing profile, averaged over the delay period. (D) Remembered cue as measured by the population vector from 20 sample trials with the same cue location. The memory traces drift away from the initial cue during the delay, the VPV across trials quantifies this deviation so that the smaller is the VPV, and the more accurate is the memory readout. (E) Drift magnitude at 5–6 s of the delay period, as measured by the VPV (N = 500 trials), is plotted as a function of the time constant of the NMDAR-mediated synaptic excitation τ_S. The VPV decreases steeply with increasing τ_S; the fitting line is an exponential function for ease of eye inspection.

Figure 2.

Tradeoff between memory accuracy and flexibility with I_CAN. (A) An integrate-and-fire neuron model endowed with I_CAN. A step current (bottom panel) induces initial firing activity (upper panel). Each spike triggers a small calcium influx (middle upper panel), which leads to a slow activation of I_CAN (middle lower panel). When the applied current stops, the high level of I_CAN activation is sufficient to induce afterdischarge of spikes. (B) Variance of the remembered cue location (VPV) during the delay period with max τ_CAN of 1 (black trace) and 3 (red trace) s (N = 500 trials). A longer time constant leads to smaller random drifts after an initial time needed for the mechanism to take effect. (C) With max τ_CAN = 500 ms, a negative pulse of 200 ms to excitatory cells is required in order to shutdown the bump state at the end of delay. Lower panel shows applied current with 2 negative pulses of lasting 100 (red) and 200 (blue) ms. Middle and upper panels: the average population firing rates and I_CAN activation, respectively, of 200 cells in the bump state around the initial cue location, under the 2 conditions (the same color scheme, N = 10 trials). With 100 ms, I_CAN activation decays by a small amount but immediately increases after the shutdown input is over, providing the necessary positive feedback for the return of the high-firing memory state. After a longer shutdown pulse (200 ms), the activation decays to such an extent that ultimately leads to the resting state. (D) State space analysis with the population rate and the I_CAN activation shown in (C) plotted against each other in phase space. Each trajectory corresponds to a trial and starts immediately at the shutdown pulse offset. Red trajectories evolve to the bump attractor; blue proceed to shutdown (resting state). There is a clear diagonal boundary that separates the 2 attractors (dashed black curve), suggesting the presence of an unstable manifold. (E) Tradeoff between decrease in variance of remembered cue location (VPV) and minimum time to shutdown (t_SHUT,MIN), with increasing max τ_CAN. Open circles were determined as in Figure 1E, with max τ_CAN between 50 ms and 4 s. Filled circles express t_SHUT,MIN (see Materials and Methods) (N = 500 trials). The 2 data sets are fitted as a sum of 2 exponentials (VPV) or as a simple exponential (t_SHUT,MIN). A compromise corresponds to an optimal value of max τ_CAN≈ 1.5 s.

Figure 3.

Tradeoff between memory accuracy and flexibility with DSI. (A) Schematic of network model of spatial working memory endowed with DSI. This mechanism is implemented as a cell-specific reduction in inhibitory input conductance. Adapted from Carter and Wang (2007). (B) Left panel: spatiotemporal pattern of excitatory cells endowed with DSI (τ_D = 5 s). Cue was presented at 180° during the 0.75–1 s interval. A shutdown pulse of 500 ms was applied at 8 s. The yellow lines represent the remembered cue location during delay and after shutdown pulse. Right panel: population firing profiles, averaged over the delay period (blue) or over the last second of the simulation (red), showing that the bump state survives the shutdown input and the memory trace is not erased. (C) Spatiotemporal representation of the activation variable (D) of DSI (inverted scale, 1 means no DSI) of the same trial. Only the (D) value of 41 cells (recorded equidistantly in the network) is plotted. The lingering DSI trace, visible after the shutdown pulse, is sufficient to induce the re-emergence of the bump state (in B). (D) The accuracy–flexibility tradeoff with DSI. The variance of the remembered cue location (VPV) during the delay period with effective τ_D of 1 (black trace) and 5 (red trace) s (N = 500 trials). In the former scenario, the VPV keeps increasing almost linearly. In contrast, in the latter, it stabilizes after an initial period of 2 s. (E) Tradeoff between decrease in the VPV (open symbols) and t_SHUT,MIN (closed circles), as τ_D is increased from 50 ms to 5 s (N = 500 trials). The VPV was determined during 2 intervals of the delay period: 5–6 s (open circles, same as Figs 1E and 2E) or 12–13 s (open squares). The data sets were fitted by solid curves for eye inspection.

Figure 4.

Multistability analysis of the working memory model as a dynamical system reveals that I_CAN and DSI increase the robustness of memory function. Simulations were ran with (black dots) or without (red dots) cue presentation, for a range of recurrent excitatory conductance (G_EE) values. The maximum firing rate among all excitatory cells, at the end of the delay period, is either low (2–6 Hz) corresponding to the resting state or higher than 20 Hz corresponding to a memory sate. The resulting state diagram is shown for the control network without slow mechanisms (A), with only DSI (B) or I_CAN (C) or both (D). The range of G_EE values for multistability are delimited by 2 vertical dashed lines. The presence of DSI (B) and I_CAN (C) alone increased the multistability range and also the firing rate separation between memory and resting states. These effects are larger when both mechanisms are combined (D).

Figure 5.

DSI and I_CAN stabilize the memory trace in the presence of heterogeneity across neurons in the network. Simulations were carried out where the cue was applied at 20 evenly spaced locations along the 360° space. The maintenance and retrieval of memory require that the remembered location at any given point in time should closely match that of the to-be-remembered cue. (A) The remembered cue locations of the simulations with the control parameter set systematically drift to a few privileged locations. (B) When DSI (4% maximum effect) and I_CAN (g_CAN = 1.5 nS) were incorporated in the network, the internal representation of the cue location becomes much better (the population vector is nearly stable across time). (C) The mean drift from the original cue location (at the end of a 9-s delay) is greatly reduced with DSI and I_CAN compared with the control (N = 500 trials). The time constant for DSI and I_CAN were, respectively, 2 and 0.5 s.

Figure 6.

STF of recurrent excitatory synapses reduces random drifts. (A) t_SHUT,MIN (filled circles) increases with τ_F (fitted with an exponential equation). Likewise, the variance of the remembered cue location (VPV) also increases with slower STF (exponential fit), but remains much smaller than that in the absence of STF (VPV = 206 deg² in Fig. 1E, τ_S = 100 ms; N = 500). (B) Steady-state profiles of F⁺ (the facilitation variable, F, after a spike) for 5 different τ_F (7 s after delay start, N = 400). For longer time constants, the peak of the profile broadens (dashed gray double arrow), resulting in a region effectively without facilitation. This explains increased drifts with longer τ_F. (C) Phase space plot of F and the population firing rate. Each trajectory corresponds to a trial and starts immediately at the shutdown pulse offset. The network either revert back to the mnemonic bump state (trials in red) or rest to the resting state (trials in blue), depending on the stochastic network dynamics. The F variable fluctuates from trial to trial and is significantly larger in red trajectories than blue ones (see Results). Note that, at the pulse offset, the population of excitatory cells was silent. However, due to the temporal sliding window (50 ms) used to calculate firing rates, the trajectories depicted start at >0 Hz.

Figure 7.

A simplified model with fixed F profile shows that the network is multistable within a range of STF values. (A) The black curve corresponds to the orange profile (τ_F = 1 s) in Figure 6B, and the other curves were obtained by assuming an exponential decay in time of the black profile, during different temporal intervals (see Results). (B) Bifurcation diagram for τ_F = 1 and 2 s (upper and lower panels, respectively). Simulations were run with (black dots) or without (red dots) cue presentation, and plotted is the maximum firing rate among all excitatory cells, at the end of the delay period. In these simulations, F did not change dynamically but was set as a parameter and given spatial profiles as those shown in (A). The peaks of the corresponding F profiles are shown in the abscissa. Below F₁, the network was always in the resting state. Above F₂, no cue was necessary to initiate a bump. (C) F₁ and F₂ as a function of τ_F = 0.5, 1, 2, 3, 4 s (fit with single exponentials). The shaded area represents the presence of multistability.

Figure 8.

STF stabilizes the remembered cue locations in the presence of heterogeneity across neurons in the network. In stimulations, the cue location was applied at 20 evenly spaced locations along the 360° space. (A) The remembered cue locations with STF (τ_F = 1 s) show visibly less drifts than the control (Fig. 5A). (B) The mean heterogeneity-induced systematic drifts (at the end of a 9-s delay) for the network model without STF (control) or with STF operating at 3 different time constants (N = 400).

Figure 9.

Slow mechanisms preserve cue representation and decrease the influence of long distractor stimuli. (A) Smoothed spatiotemporal activity pattern of the network's excitatory cells under control conditions (upper panel) or with DSI (lower panel), in the presence of a distractor. An initial cue stimulus (peak angle θ_S = 180°, 750 ms–1 s, first pair of vertical dashed lines) drives the network to the memory state. The application of a distractor during the delay period (peak angle θ_D = 300°, 100 pA, 6–6.25 s, second pair of dashed lines) pulls the location of the bump closer to it. In these 2 example trials, the deviation of the bump, measured as the difference between the remembered cue location after the distractor (θ₂, 8 – 9 s) and before (θ₁, 4.5–5.5 s), is larger in the control network than with DSI. (B) The average difference between θ₂ and θ₁ as a function of the difference in peak angles of distractor (θ_D) and cue stimulus (θ_S), for 3 distractor durations (N = 150). The deviation increases and approaches the perfect distraction (diagonal dashed line) before declining for more distant distractors. Longer durations produce generally larger deviations that have a maximum at larger distractor angles. (C) Same as in (B) but for network with DSI. The differences in remembered cue locations are visibly smaller than with the control network for all 3 distractor durations (N = 150). (D) Distraction indicators for sets of trials with different distractor durations, under control network (grey symbols) or with DSI (black symbols). Upper panel: the maximum distraction is small and increases almost linearly in a network with DSI. Under control conditions, this measure is larger throughout the whole range and has a more prominent increase. The edge-colored data points were taken from (B) and (C) with the same color scheme. Lower panel: similarly, the distraction angle (θ_D− θ_S) at which the maximum deviation of the bump is observed is wide and increases with duration in the control network, but is narrower and almost stable when DSI is present. This slow mechanism limits the effects of closer distractors and protects the memory against farther ones almost independently of their duration.

Figure 10.

Schematic phase-plane diagram of our working memory model, during 3 stages of a shutdown process. This scheme applies to all 3 slow biophysical mechanisms considered in this paper, with X representing the activation variable of I_CAN, DSI, or STF. The inset in (B) displays the timing of the 3 stages according to the presentation of the negative shutdown input. (A) The state space displays a stable manifold (line with converging arrows) and an unstable manifold (line with diverging arrows), and their intersection creates a saddle point. There are 2 stable steady states (filled circle) representing a memory state and a rest state. At the end of delay, the system is in the memory state. (B) During the application of the negative pulse, there is only one steady state (filled circle), with a low-firing rate and low X magnitude. After the quick suppression of all firing activity (“FAST”), the system moves along the direction of the exponential decay of X (“SLOW”) over the duration of the pulse. (C) The attractor landscape (A) is restored after the pulse offset. Depending on whether the state of the system at the offset of the shutdown input is on the left or the right side of the stable manifold, the system will revert back to the memory state (red trajectory) or reset to the resting state (blue trajectory, successful shutdown).