In-vivo measurement of muscle tension: dynamic properties of the MC sensor during isometric muscle contraction

Abstract

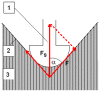
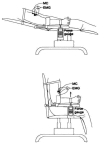
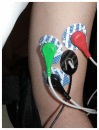
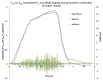
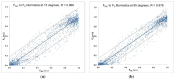
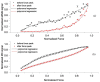
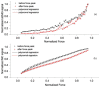
Skeletal muscle is the largest tissue structure in our body and plays an essential role for producing motion through integrated action with bones, tendons, ligaments and joints, for stabilizing body position, for generation of heat through cell respiration and for blood glucose disposal. A key function of skeletal muscle is force generation. Non-invasive and selective measurement of muscle contraction force in the field and in clinical settings has always been challenging. The aim of our work has been to develop a sensor that can overcome these difficulties and therefore enable measurement of muscle force during different contraction conditions. In this study, we tested the mechanical properties of a "Muscle Contraction" (MC) sensor during isometric muscle contraction in different length/tension conditions. The MC sensor is attached so that it indents the skin overlying a muscle group and detects varying degrees of tension during muscular contraction. We compared MC sensor readings over the biceps brachii (BB) muscle to dynamometric measurements of force of elbow flexion, together with recordings of surface EMG signal of BB during isometric contractions at 15° and 90° of elbow flexion. Statistical correlation between MC signal and force was very high at 15° (r = 0.976) and 90° (r = 0.966) across the complete time domain. Normalized SD or σN = σ/max(FMC) was used as a measure of linearity of MC signal and elbow flexion force in dynamic conditions. The average was 8.24% for an elbow angle of 90° and 10.01% for an elbow of angle 15°, which indicates high linearity and good dynamic properties of MC sensor signal when compared to elbow flexion force. The next step of testing MC sensor potential will be to measure tension of muscle-tendon complex in conditions when length and tension change simultaneously during human motion.

Figure 1.

A simplified representation of the muscle contraction sensor (MC) measuring principle for the determination of the mechanical and physiological properties of skeletal muscles (1): Sensor tip; (2): Skin and intermediate layer; (3): Measured muscle.

Figure 2.

Measurement setup. Measurements were performed at two different elbow angles: 15° and 90°.

Figure 3.

Position of MC sensor (black) and EMG electrodes on m. biceps brachii.

Figure 4.

Simultaneously recorded F_MC, F_D and EMG during isometric contraction of biceps brachii muscle of subject 3 (n3). Coefficient sensitivity of the system k_opt (see Section 2.7) was used for normalization of F_D signal (F_MC ≈ kF_D).

Figure 5.

(a) Scatter plot of normalized F_MC an F_D signal at 15° elbow flexion with regression line and confidence bands at 0.95. Correlation coefficient was R = 0.966; (b) Scatter plot of normalized F_MC an F_D signal at 90° elbow flexion with regression line and confidence bands at 0.95. Correlation coefficient was R = 0.976.

Figure 6.

(a) Each point on curves is the average of all records of the mean normalized sEMG, obtained when F_D was within 2% of each chosen force value (0.02, 0.4…to 0.98 at elbow angle 15°) while the force was rising (i.e., before the peak, black colour) or while force was falling (i.e., after the peak, red colour). Bars show SEM, and line is polynomial regression of the relationship between F_MC and F_D, before the peak (adjusted R² = 0.96) and red line after the peak (adjusted R² = 0.96); (b) Each point on the curves is the average of all records of the mean normalized F_MC, obtained when F_D was within 2% of each chosen force value (0.02, 0.4…to 0.98 at elbow angle 15°) while the force was rising (i.e., before the peak, black colour) or while force was falling (i.e., after the peak, red colour). Bars show SEM, and line is polynomial regression of the relationship between F_MC and F_D, before the peak (adjusted R² = 0.99) and red line after the peak (adjusted R² = 1).

Figure 7.

(a) Each point on curves is the average of all records of the mean normalized sEMG, obtained when F_D was within 2% of each chosen force value (0.02, 0.4…to 0.98 at elbow angle 90°) while the force was rising (i.e., before the peak, black colour) or while force was falling (i.e., after the peak, red colour). Bars show SEM, and line is polynomial regression of the relationship between F_MC and F_D, before the peak (adjusted R² = 0.96) and red line after the peak (adjusted R² = 0.96); (b) Each point on curves is the average of all records of the mean normalized F_MC, obtained when F_D was within 2% of each chosen force value (0.02, 0.4…to 0.98 at elbow angle 90°) while the force was rising (i.e., before the peak, black colour) or while force was falling (i.e., after the peak, red colour). Bars show SEM, and line is polynomial regression of the relationship between F_MC and F_D, before the peak (adjusted R² = 0.99) and red line after the peak (adjusted R² = 0.99).