Mechanism and function of mixed-mode oscillations in vibrissa motoneurons

Abstract

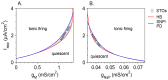
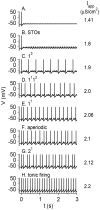
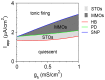
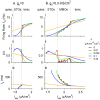
Vibrissa motoneurons in the facial nucleus innervate the intrinsic and extrinsic muscles that move the whiskers. Their intrinsic properties affect the way they process fast synaptic input from the vIRT and Bötzinger nuclei together with serotonergic neuromodulation. In response to constant current (I(app)) injection, vibrissa motoneurons may respond with mixed mode oscillations (MMOs), in which sub-threshold oscillations (STOs) are intermittently mixed with spikes. This study investigates the mechanisms involved in generating MMOs in vibrissa motoneurons and their function in motor control. It presents a conductance-based model that includes the M-type K+ conductance, g(M), the persistent Na+ conductance, g(NaP), and the cationic h conductance, g(h). For g(h) = 0 and moderate values of g(M) and g(NaP), the model neuron generates STOs, but not MMOs, in response to I(app) injection. STOs transform abruptly to tonic spiking as the current increases. In addition to STOs, MMOs are generated for g(h)>0 for larger values of I(app); the I(app) range in which MMOs appear increases linearly with g(h). In the MMOs regime, the firing rate increases with I(app) like a Devil's staircase. Stochastic noise disrupts the temporal structure of the MMOs, but for a moderate noise level, the coefficient of variation (CV) is much less than one and varies non-monotonically with I(app). Furthermore, the estimated time period between voltage peaks, based on Bernoulli process statistics, is much higher in the MMOs regime than in the tonic regime. These two phenomena do not appear when moderate noise generates MMOs without an intrinsic MMO mechanism. Therefore, and since STOs do not appear in spinal motoneurons, the analysis can be used to differentiate different MMOs mechanisms. MMO firing activity in vibrissa motoneurons suggests a scenario in which moderate periodic inputs from the vIRT and Bötzinger nuclei control whisking frequency, whereas serotonergic neuromodulation controls whisking amplitude.

Figure 1. Bifurcation diagrams of the vibrissa motoneuron model with g _h = 0.

The values of the membrane potential V (top panels) and the firing rate f _R (medium panels) are plotted as functions of I _app for fixed points (thin lines) and limit cycles (thick lines) for g _M = 0.4 mS/cm² (A), g _M = 1 mS/cm² (B) and g _M = 1.4 mS/cm² (C). For limit cycles, minimal and maximal voltages during the cycle are plotted. Solid lines denote stable solutions, and dotted lines denote unstable solutions. Stable sub-threshold oscillations are shown in blue, whereas stable tonic firing states are shown in solid thick black lines. Solid circles denote bifurcations from the following types: Hopf (HB), saddle-node of periodics (SNP) and period doubling (PD). Panels B₁-B₃ at the bottom present the voltage time traces for g _M = 1 mS/cm² and I _app = 1.4, 1.6 and 1.8 µA/cm² respectively. These I _app values are denoted by the arrows below the abscissa in panel B (top).

Figure 2. Phase diagrams of the vibrissa motoneuron model with g _h = 0.

The dynamical states of the model neuron are plotted in the g _M-I _app plane (A) and in the g _M-I _app plane (B). A regime of STOs (light grey) is obtained between the regimes of quiescence and tonic firing. Red lines denote the Hopf bifurcation (HB), and blue lines denote the saddle-node of periodics (SNP) or period doubling (PD) bifurcations.

Figure 3. Bifurcation diagrams of the vibrissa motoneuron model with g _h = 0.3 mS/cm².

(A) The values of the membrane potential V (top panel) and the firing rate f _R (bottom panel) are plotted as functions of I _app for fixed points (thin lines) and limit cycles (thick lines) for g _M = 1 mS/cm². For limit cycles, minimal and maximal voltages during the cycle are plotted. Solid lines denote stable solutions, and dotted lines denote unstable solutions. Stable sub-threshold oscillations are shown in blue, whereas stable tonic firing states are shown in solid thick black lines. Solid circles in the top panels denote bifurcations from the following types: Hopf (HB), saddle-node of periodics (SNP) and period doubling (PD). The firing rate in the MMOs state is plotted in red in the bottom panel. (B) The firing rate f _R in the MMOs state is plotted as a function of I _app at a larger scale. The types of mixed mode states (see text, Figure 4 and [23]) are indicated above the curve.

Figure 4. Voltage time traces of the model neuron in response to step current injection at t = 0.

Parameters are as in Figure 3 (g _h = 0.3 mS/cm²). The values of I _app are written in units of µA/cm². (A) I _app = 1.41, the membrane potential of the neuro goes to rest. (B) I _app = 1.8, the neuron exhibits sub-threshold oscillations. (C) I _app = 1.9, the neuron fires in an MMOs mode, with 3 sub-threshold oscillations between each pair of consecutive spikes. (D) I _app = 2.0, the neuron fires in an MMOs mode. The number of STOs between pairs of consecutive spikes switches alternately between 1 and 2. (E) I _app = 2.06, the neuron fires in an MMOs mode with one STO between two consecutive spikes. (F) I _app = 2.1, the neuron fires aperiodically. (G) I _app = 2.12, The neuron fires two spikes, shows one STO, and then the cycle starts again. (H) I _app = 2.2, the neuron fires tonically. The dynamical states are indicated above each panel.

Figure 5. Phase diagram of the vibrissa motoneuron model in the g _h-I _app plane.

Regimes of STOs (light grey) and MMOs (dark grey) are obtained between the regimes of quiescence and tonic firing. The red line denotes Hopf bifurcation (HB), the green line denotes period doubling (PD) bifurcation, and the blue line denotes saddle-node of periodics (SNP) bifurcation.

Figure 6. Voltage fluctuations generated by stochastic noise.

(A) Voltage time traces of the model neurons with g _M = 1 mS/cm², g _NaP = 0.04 mS/cm², g _h = 0, I _app = 1.4 µA/cm², σ = 0.032 µA×ms^1/2/cm². For σ = 0, the model neurons are at rest for this parameter set. With noise, the membrane potential fluctuates. (B) The standard deviation of the voltage σ_V as a function of the noise level σ. This figure demonstrates how the noise strength affects the magnitude of voltage fluctuations without any intrinsic STOs mechanism.

Figure 7. Voltage time traces of the model neuron in response to step current injection at t = 0.

The values of I _app are indicated to the right of the traces. (A) g _h = 0, σ = 0.01 µA×ms^1/2/cm². The noiseless neuron does not exhibit MMOs, but this level of noise generates MMOs near the transition between quiescence and tonic firing. (B) g _h = 0, σ = 0.1 µA×ms^1/2/cm². For this larger noise level, MMOs are generated in a more widespread I _app regime. (C) g _h = 0.3 mS/cm², σ = 0.01 µA×ms^1/2/cm². The noiseless neuron generates MMOs. This level of noise increases the I _app regime in which MMOs are obtained only slightly. The MMOs are less ordered, and the number of STOs between spikes varies from one inter-spike interval to another. (D) g _h = 0.3 mS/cm², σ = 0.1 µA×ms^1/2/cm². MMOs appear in I _app regimes in which the noiseless neuron is quiescent or fires tonically, and the firing patterns look less ordered.

Figure 8. Properties of firing patterns without and with an intrinsic MMOs-generating mechanism.

The firing rate f _R (I), the coefficient of variation CV (II) and the time period t _p, computed assuming a Bernoulli process (Equation 3) (III) are plotted as a function of I _app for g _h = 0 (A) and g _h = 0.3 mS/cm² (B). The colors of the lines denoting the values of σ (in µA×ms^1/2/cm²) are: black – 0, red – 0.01, green – 0.032, blue – 0.1 and orange – 0.32. The vertical dotted lines denote the I _app values of the transitions between different dynamical states (quiescence, STOs, MMOs and tonic firing) of the noiseless neuron.

Figure 9. Response of a motoneuron pool to periodic stimulation from a CPG and neuromodulation.

50 uncoupled motoneurons are simulated, each receiving constant input I _app = 2 µA/cm² mimicking the excitability effects of neuromodulators such as serotonin, and periodic stimulation from a CPG with a frequency f = 10 Hz. The periodic stimulation is I _c = 0.15 µA/cm² during the first 20 ms of each cycle with a duration of T _per = 1/f, and 0 otherwise. Different neurons have different noise realizations. Additional parameters: g _h = 0.3 mS/cm², σ = 0.032 µA×ms^1/2/cm². Realizations of the noise are different across motoneurons. (A) The membrane potential V as a function of t for two neurons (black). The stimulus pattern is schematically plotted above each panel (red) to emphasize the synchrony of spikes with the stimulus. (B) Rastergram of the spikes (black circles) of the 50 motoneurons. The stimulus is I _c between each pair of adjacent red lines. (C) The total force amplitude F, in arbitrary units (A = 1, Equation 4), generated by a whole muscle whose cells are innervated by the pool of motoneurons (black). The dotted blue line denotes a similar simulation with I _app = 2.4 µA/cm².