Self-consistent determination of the spike-train power spectrum in a neural network with sparse connectivity

Abstract

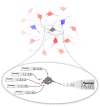
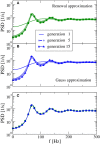
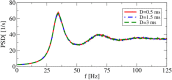
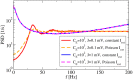
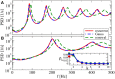
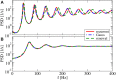
A major source of random variability in cortical networks is the quasi-random arrival of presynaptic action potentials from many other cells. In network studies as well as in the study of the response properties of single cells embedded in a network, synaptic background input is often approximated by Poissonian spike trains. However, the output statistics of the cells is in most cases far from being Poisson. This is inconsistent with the assumption of similar spike-train statistics for pre- and postsynaptic cells in a recurrent network. Here we tackle this problem for the popular class of integrate-and-fire neurons and study a self-consistent statistics of input and output spectra of neural spike trains. Instead of actually using a large network, we use an iterative scheme, in which we simulate a single neuron over several generations. In each of these generations, the neuron is stimulated with surrogate stochastic input that has a similar statistics as the output of the previous generation. For the surrogate input, we employ two distinct approximations: (i) a superposition of renewal spike trains with the same interspike interval density as observed in the previous generation and (ii) a Gaussian current with a power spectrum proportional to that observed in the previous generation. For input parameters that correspond to balanced input in the network, both the renewal and the Gaussian iteration procedure converge quickly and yield comparable results for the self-consistent spike-train power spectrum. We compare our results to large-scale simulations of a random sparsely connected network of leaky integrate-and-fire neurons (Brunel, 2000) and show that in the asynchronous regime close to a state of balanced synaptic input from the network, our iterative schemes provide an excellent approximations to the autocorrelation of spike trains in the recurrent network.

Keywords: neural noise; non-Poissonian spiking; recurrent neural networks; spike-train power spectrum; spike-train statistics.

Figure 1

Basic problem addressed in this paper. Excitatory (red) and inhibitory (blue) neurons interacting in a recurrent network (top) fire spike trains with a temporal correlation that can be characterized by the spike-train power spectrum. We focus on a homogeneous network, in the sense that excitatory and inhibitory neurons share the same firing rate and power spectrum. At the single-cell level (magnification at the bottom), a neuron is driven by a superposition of spike trains, the power spectra of which should be equal to the power spectrum of the neuron itself. This poses a self-consistency problem that we attempt to solve numerically in this paper in different approximations.

Figure 2

Power spectra resulting from the self-consistent procedure. For balanced input from the previous generation (g = 4) and a large presynaptic environment (C_E = 10³, C_I = 250) both the renewal approximation (A) and the Gaussian approximation (B) have converged to unique stationary spectra, which are compared in (C). In the first generation, the neuron is stimulated by a constant input 〈RI(t)〉 = 30 mV and C_E + C_I Poissonian spike trains of rate ν_in = 71 Hz [solution for the self-consistent firing rate Equation (13)] with amplitude J = 0.1 mV (excitatory synapses) and −gJ = −0.4 mV (inhibitory synapses). Note the rapid convergence of spectra for both approximations: the spectrum of the fifth generation differs only slightly from the result for the 15th generation.

Figure 3

Evolution of ISI statistics over generations in stable (A,B,C,F) and unstable (D,E,G) regimes. Starting with Poissonian spike trains in the zeroth generation, the nth generation of the LIF neuron (n ≥ 1) receives noise input according to the statistics of the previous generation. Parameters as in Figure 2 yield the same stable rate (A) and CV (B) irrespective of whether the initial Poisson stimulation (zeroth generation) of the first generation (LIF neuron) is 15 or 71 Hz. The first serial correlation coefficient is positive for both procedures but differs in magnitude (C). Increasing the relative strength of inhibition to g = 5, our scheme is not stable anymore and both rate (D) and CV (E) oscillate as functions of the generation. Stability can be discussed in terms of the firing rate Equation 13 shown in (F,G) vs. input rate (black line) together with the identity line. In the regime of (A–C), the map from input rate to output rate (F) has a stable fixed point and small perturbations from it (magenta point) relax back into the fixed point (blue arrows). In the regime of (D–E), small perturbations are amplified (G), yielding an unstable fixed point.

Figure 4

Delay dependence of power spectra in recurrent networks. Asynchronous regime. Parameters: (g = 4.5), and (v_R = 10 mV).

Figure 5

System-size dependence of power spectra in recurrent networks. Asynchronous regime for (g = 4.5), and (v_R = 10 mV).

Figure 6

Synaptic-amplitude dependence of power spectra and difference between external constant and shot-noise input. Asynchronous regime for (g = 4.5) and (v_R = 10 mV).

Figure 7

Power spectra for dominating network excitation. Results of recurrent network simulations and the two approximations from our iterative schemes for g = 3.5 (excitatory local synaptic input). (A) v_R = 0 mV (firing rate ν = 86.1 Hz, C_V = 0.045); (B) v_R = 10 mV (firing rate ν = 202.5 Hz, C_V = 0.10). Inset shows serial correlation coefficients for (B).

Figure 8

Power spectra for balanced network input. Results of recurrent network simulations and the two approximations from our iterative schemes for (g = 4) (balanced local synaptic input). (A) (v_R = 0 mV) [firing rate ν = 44.5 Hz, C_V = 0.05] and (B) (v_R = 10 mV) (firing rate ν = 70.4 Hz, C_V = 0.19).

Figure 9

Power spectra for dominating network inhibition. Results of recurrent network simulations and the two approximations from our iterative schemes for g = 4.5 (inhibitory local synaptic input). (A) v_R = 0 mV (firing rate ν = 28.1 Hz, C_V = 0.088); (B) v_R = 10 mV (firing rate ν = 34.8 Hz, C_V = 0.27). Inset shows serial correlation coefficients for (B).

Figure 10

Effect of larger synaptic amplitude on power spectra. Results of recurrent network simulations and the two approximations from our iterative schemes for a synaptic amplitude of J = 1 mV, a smaller number of synapses C_E = 100, C_I = 25, and (g = 4.5) (inhibitory local synaptic input). (A) (v_R = 0 mV) (firing rate ν = 38.6 Hz, C_V = 0.58); (B) (v_R = 10 mV) (firing rate ν = 65.7 Hz, C_V = 1.98).