Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2014 Oct 7;9(10):e109166.
doi: 10.1371/journal.pone.0109166. eCollection 2014.

A Compound fault diagnosis for rolling bearings method based on blind source separation and ensemble empirical mode decomposition

Huaqing Wang  1 , Ruitong Li  1 , Gang Tang  1 , Hongfang Yuan  2 , Qingliang Zhao  1 , Xi Cao  2
Affiliations

A Compound fault diagnosis for rolling bearings method based on blind source separation and ensemble empirical mode decomposition

Huaqing Wang et al. PLoS One. .

Abstract

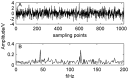
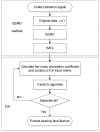
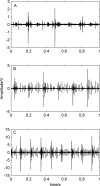
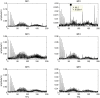
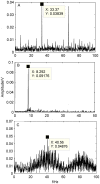
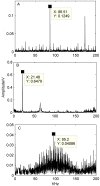
A Compound fault signal usually contains multiple characteristic signals and strong confusion noise, which makes it difficult to separate week fault signals from them through conventional ways, such as FFT-based envelope detection, wavelet transform or empirical mode decomposition individually. In order to improve the compound faults diagnose of rolling bearings via signals' separation, the present paper proposes a new method to identify compound faults from measured mixed-signals, which is based on ensemble empirical mode decomposition (EEMD) method and independent component analysis (ICA) technique. With the approach, a vibration signal is firstly decomposed into intrinsic mode functions (IMF) by EEMD method to obtain multichannel signals. Then, according to a cross correlation criterion, the corresponding IMF is selected as the input matrix of ICA. Finally, the compound faults can be separated effectively by executing ICA method, which makes the fault features more easily extracted and more clearly identified. Experimental results validate the effectiveness of the proposed method in compound fault separating, which works not only for the outer race defect, but also for the rollers defect and the unbalance fault of the experimental system.

PubMed Disclaimer

Conflict of interest statement

Competing Interests: The authors have declared that no competing interests exist.

Figures

Figure 1
Figure 1. Flowchart of EEMD algorithm.
Figure 2
Figure 2. Original simulated signal and its spectrum.
A) waveform of original simulated signal; B) spectrum of the original simulated signal.
Figure 3
Figure 3. IMF components decomposed by EEMD method.
Figure 4
Figure 4. Spectra of separated signals by the proposed method.
A) spectrum of IC1; B) spectrum of IC2.
Figure 5
Figure 5. Flowchart of the experiment scheme.
Figure 6
Figure 6. Experimental system for bearing diagnosis.
Figure 7
Figure 7. Install location of the acceleration sensor.
Figure 8
Figure 8. Original diagnosis signal waveforms at different rotating speed.
A) at 500 rpm; B) 900 rpm; C) 1300 rpm.
Figure 9
Figure 9. Envelope spectra of the original signal at different rotating speed.
A) 500 rpm; B)900 rpm; B)1300 rpm.
Figure 10
Figure 10. Envelope spectra of each level wavelet coefficients.
Figure 11
Figure 11. Envelop spectra of IMF1–IMF6.
Figure 12
Figure 12. Spectra of the separated signals by the proposed method at 900 rpm.
A) spectrum of the outer-race defect; B) spectrum of the unbalance fault; C) spectrum of the rollers defect.
Figure 13
Figure 13. Spectra of the separated signals by the proposed method at 500 rpm.
A) Spectrum of the outer-race defect; B) Spectrum of the unbalance fault; C) Spectrum of the rollers defect.
Figure 14
Figure 14. Spectra of the separated signals by the proposed method at 1300 rpm.
A) Spectrum of the outer-race defect; B) Spectrum of the unbalance fault; C) Spectrum of the rollers defect.
See this image and copyright information in PMC

References

    1. Hongbin M (1995) Rolling bearing vibration detection and diagnosis. Beijing: Machine Press.
    1. Herault J, Jutten C (1986) Space or time adaptive signal processing by neural network models. Proceedings of the AIP Neural Networks for Computing 151: 206–211.
    1. Friman O, Borga M, Lundberg P, Knutsson H (2002) Exploratory fMRI analysis by autocorrelation maximization. NeuroImage 16: 454–464. - PubMed
    1. Li M, Liu YD, Feng GY, Zhou ZT, Hu DW (2010) OI and fMRI signal separation using both temporal and spatial autocorrelations. IEEE Transactions on biomedical engineering 57: 1917–1925. - PubMed
    1. Lee T, Lewicki MS, Girolami M (1999) Blind source separation of more sources than mixtures using overcomplete representations. IEEE Signal Processing Letters 6: 87–90.

Publication types

MeSH terms

LinkOut - more resources