Cancer evolution: mathematical models and computational inference

Abstract

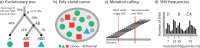
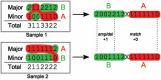
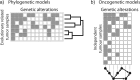
Cancer is a somatic evolutionary process characterized by the accumulation of mutations, which contribute to tumor growth, clinical progression, immune escape, and drug resistance development. Evolutionary theory can be used to analyze the dynamics of tumor cell populations and to make inference about the evolutionary history of a tumor from molecular data. We review recent approaches to modeling the evolution of cancer, including population dynamics models of tumor initiation and progression, phylogenetic methods to model the evolutionary relationship between tumor subclones, and probabilistic graphical models to describe dependencies among mutations. Evolutionary modeling helps to understand how tumors arise and will also play an increasingly important prognostic role in predicting disease progression and the outcome of medical interventions, such as targeted therapy.

Keywords: Cancer; cancer progression; evolution; population genetics; probabilistic graphical models.

Figure 1.

Common aberrations in cancer genomes. These events lead to the abnormal chromosome numbers (aneuploidy) and chromosome structures of a cancer genome. Lines indicate the genome with germline genome on top and cancer genome with somatic aberrations below. Double lines are used when differentiating heterozygous and homozygous changes is useful. Dots represent single nucleotide changes, whereas lines and arrows represent structural changes.

Figure 2.

Modeling the population dynamics of cancer cells. a) Schematic illustration of the genetic progression from initially healthy cells (normal cells) to an invasive cancer by accumulating driver mutations. b) Age-incidence curves rise sharply above the age of 50 and are informative about the dynamics of tumor progression. The straight line shows a fit with power 4.8. The log-log-linear dependency of incidence on age is used in multistage theory to estimate the number of rate-limiting steps in cancer progression from incidence data. c) Population genetics models such as the Wright–Fisher model can be used to model the accumulation of driver mutations through multiple clonal expansions and to derive the average waiting times ${\tau }_k$ for a given number of alterations $k$. d) Dynamics of a three-strategy game corresponding to cell types A, B, and C. While simple additive fitness models always lead to the survival of the fittest, evolutionary game theory accounts for cellular interactions and allows for more complex dynamics, such as stable coexistence of cell types. Indicated here is a stable equilibrium with strategy A and C, but not B, which is reached from all three starting conditions via the indicated evolutionary paths.

Figure 3.

Inferring tumor phylogeny from next-generation sequencing data. a) Subclones are related to each other by an evolutionary process of acquisition of mutations. In this example, the three clones (leaf nodes) are characterized by different combinations of the four single nucleotide variant (SNV) sets $A$, $B$, $C$, and $D$. The percentages on the edges of the tree indicate the fraction of cells with this particular set of SNVs, e.g., 70% of all cells carry $A$, 40% additionally carry $B$, and only 7% carry $A$, $B$, and $D$. b) The evolutionary history of a tumor gives rise to a heterogeneous collection of normal cells (small discs) and cancer subclones (large discs, triangles, squares). Internal nodes that have been fully replaced by their descendants (like the one carrying SNV sets $A$ and $B$ without $C$ or $D$) are no longer part of the tumor. c) Sequencing data consist of short reads covering (parts of) the cancer genome. Comparison to the germline DNA of the same patient allows to identify SNVs and other genomic aberrations. Since reads are short, most will only cover a single SNV. In few cases, pairs of SNVs are covered, which allows to assess patterns of co-occurrence and mutual exclusivity between SNVs. d) The sets of SNVs distinguishing the subclones cluster in the SNV frequency distribution. The mean of each cluster ($x$-axis) is the fraction of cells carrying this set of SNVs. The goal of tumor phylogenetics is to infer the evolutionary tree (a) from the mutations observed in the sequencing data (c) and their frequencies (d).

Figure 4.

Two simple principles for tree inference from SNVs. For a given set of subclones and their respective clonal fractions, each illustrated by a triangle with a dot at the top vertex representing the clonal origin, two conditions need to be met for a potential phylogeny to be considered feasible: a) Dirichlet's box: If two SNV frequencies (small triangles inside large triangle) sum to more than 100%, then some cancer cells must contain both SNVs (overlap of the two small triangles). In a tree-like evolutionary process some cells must have acquired the same mutation independently, which in cancer, is considered highly unlikely. Hence, one of the two subclones (small triangles) is ancestral to the other. b) Larger ancestor: In this case, if one clonal fraction is larger than the other, the larger must be the ancestor; otherwise cancer cells would have lost the previously gained mutation (nonoverlapping regions between the two small triangles at the bottom), which again is considered highly unlikely. The most likely feasible solution is shown in c), where both principles are met (and the two small triangles are nested).

Figure 5.

Phasing copy number profiles. While SNP arrays are capable of determining a major and minor copy number for the two parental alleles, their assignment (phasing) to the two actual physical alleles A and B is unknown. Because evolutionary events happen on the physical copies, correct phasing is essential for determining evolutionary distances. In this example, the two major copy number profiles between sample 1 and sample 2 (left) have a distance of two events (one amplification at position 1 and one amplification spanning positions 4 and 5), while the minor copy number profiles are identical, yielding a total of two events between the genomes of sample 1 and sample 2. Optimal assignment (right) to the alleles A and B reduces the evolutionary distance to a single amplification event spanning the first five genomic loci. This is also not evident from the total copy number (the sum of major and minor) which would still require two separate events.

Figure 6.

Phylogenetic versus oncogenetic models. Phylogenetic models of tumor samples (a) and oncogenetic models of cancer drivers (b) use the same type of data: genomic aberrations observed in patient tumor samples. Phylogenetic models (a) use mostly genomewide data of a small number of evolutionary-related tumor samples, either from the same patient or from different clones within the same tumor. Tumor progression models (b), on the other hand, generally concentrate on a small number of aberrations observed in a larger number of independent tumors from different patients.