The mechanism of phagocytosis: two stages of engulfment

Abstract

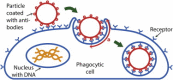
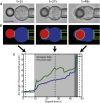
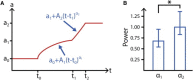
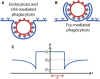
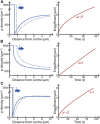
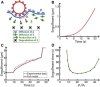
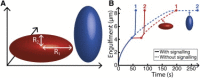
Despite being of vital importance to the immune system, the mechanism by which cells engulf relatively large solid particles during phagocytosis is still poorly understood. From movies of neutrophil phagocytosis of polystyrene beads, we measure the fractional engulfment as a function of time and demonstrate that phagocytosis occurs in two distinct stages. During the first stage, engulfment is relatively slow and progressively slows down as phagocytosis proceeds. However, at approximately half-engulfment, the rate of engulfment increases dramatically, with complete engulfment attained soon afterwards. By studying simple mathematical models of phagocytosis, we suggest that the first stage is due to a passive mechanism, determined by receptor diffusion and capture, whereas the second stage is more actively controlled, perhaps with receptors being driven toward the site of engulfment. We then consider a more advanced model that includes signaling and captures both stages of engulfment. This model predicts that there is an optimum ligand density for quick engulfment. Further, we show how this model explains why nonspherical particles engulf quickest when presented tip-first. Our findings suggest that active regulation may be a later evolutionary innovation, allowing fast and robust engulfment even for large particles.

Figure 1

Phagocytosis of a target particle. Receptors on the cell surface bind ligand molecules on the target, such as a pathogen, dead cell, or bead. As receptors bind more and more ligand molecules, the cell membrane progressively engulfs the target. Upon full engulfment, a phagosome is formed, which fuses with lysosomes, leading to digestion of the target. We denote the arc length of engulfed membrane by a, which gradually increases during engulfment. To see this figure in color, go online.

Figure 2

Typical time-lapse movie and image analysis of neutrophil engulfing an IgG-coated bead. Here the bead has diameter 4.6 μm. Data from Herant et al. (14). (A) Raw images of three frames at various stages of engulfment. At t≈2 s, the bead has been released onto the cell, with a contact area of a≈2 μm. At this point engulfment has not yet started. At t≈27 s, the bead is approximately half-engulfed, with the lower lobe noticeably ahead of the upper lobe. At t≈48 s, engulfment is complete, the bead is entirely within the cell, and the phagosome is fully formed. Scale bar: 5 μm. (B) The same frames as in panel A after automatic image analysis. (Blue) Cell; (red) bead; (green) outline of the pipette; (yellow) membrane attached to the bead. (C) Engulfment as a function of time. For both the upper and lower lobes, after engulfment begins at t≈10 s, there is an initial slow stage (light gray) followed by a much quicker second stage (dark gray). Engulfment is complete by t≈46 s. To see this figure in color, go online.

Figure 3

Fitting to the general model. (A) The general two-stage model is split into four regions. First, before engulfment begins, the contact length is constant with a = a₀. Second, after engulfment begins at t = t₀, the engulfed arc length is given as a power law with power α₁ and prefactor A₁. Third, after t = t₁, the second step begins and a is described by an independent power law with power α₂ and prefactor A₂. Fourth, after t = t₂, the particle is completely engulfed and a = a₂. (B) Comparison of the two powers, α₁ and α₂, showing the median and upper and lower quartiles. $n_{{\alpha }_1}=n_{{\alpha }_2}=12$ (6 beads × 2 lobes). A Mann-Whitney U-test showed that the difference between α₁ and α₂ is significant (p < 0.02, U = 107.5). To see this figure in color, go online.

Figure 4

Types of phagocytosis and the model variables. (A) In CR3-mediated phagocytosis, the particle sinks into the cell, in a manner similar to endocytosis. (B) In contrast, in Fcγ-mediated phagocytosis, the membrane extends via pseudopod extensions outwards around the particle. Despite these differences, we believe that the movement of receptors within the membrane is similar in both cases, and can be described by the same simple model. (C) Sketch of the receptor density, ρ, which depends only on the distance from the center of the cup, r, and the time, t. Within the cup, which has arc length a, the receptor density is always fixed at ρ_L, whereas the density at infinity, which is the same as the initial density, is ρ₀. At the edge of the cup, the receptor density is fixed at ρ₊, which is calculated by considering the free energy. In the pure diffusion model, ρ₊ is always less than ρ₀, so that receptors always flow in toward the cup and increase the cup size. To see this figure in color, go online.

Figure 5

Results from the pure diffusion, pure drift, and diffusion-and-drift models. (Left) Receptor density profile. (Right) Engulfment against time. (A) Pure diffusion model with D = 1 μm² s⁻¹. The receptor density, ρ, drops significantly just outside the cup so that ρ₊ < ρ₀ and evolves to the right as engulfment proceeds. Note that the parameters are such that ρ₊ ≈ 0. The engulfment increases as the square-root of time. Receptor profile shown at t = 3 s (solid) and t = 6 s (dashed). (B) Pure drift model with v = 0.1 μm s⁻¹. The receptor density has a completely different profile and decreases away from the cup, with ρ₊ now greater than ρ₀. Importantly, the engulfment now increases linearly in time. Receptor profile shown at t = 10 s (solid) and t = 20 s (dashed). (C) Diffusion and drift model with D = 1 μm² s⁻¹ and v = 0.1 μm s⁻¹. Engulfment now proceeds as a mixture of the pure diffusion and pure drift cases. Initially, when the receptor density is low, $a\sim \sqrt{t}$ as in the pure diffusion model. At later times, when the receptor gradient near the cup becomes approximately constant, a becomes more linear in time and behaves more like the pure drift result. Receptor profile shown at t = 3 s (solid) and t = 6 s (dashed). Parameters are ρ₀ = 50 μm⁻², ρ_L = 5000 μm⁻², $\mathcal{E}$ = 15, $\mathcal{B}$ = 20, R = 2 μm, and L = 50 μm. To see this figure in color, go online.

Figure 6

Engulfment model with signaling. (A) Sketch of the model which, in addition to the receptor density ρ, contains a signaling molecule with density S. Receptors can only diffuse (with diffusion constant D) and drift (with speed v), whereas the signaling molecule is produced within the cup with rate βρ_L, degraded everywhere with lifetime τ, and diffuses with diffusion constant D_S. (B) In contrast to other models, the rate of engulfment can now accelerate if the drift velocity depends linearly on S via v = v₁S, tending to a constant as t → ∞. Parameters are v₁ = 20 μm³ s⁻¹, β = 0.1 s⁻¹, τ = 10 s, and R = 2 μm, no diffusion. (C) In the full model, with a drift velocity that depends on the signaling molecule via a threshold, S₀, and an initial latent period, t₀, a sharp increase in engulfment rate can be obtained, which matches well with the measured data. Here the measured data is the average of the upper and lower lobes for the 4.6-μm bead shown in Fig. 2C. Parameters are D = 3.8 μm² s⁻¹, v₁ = 6 μm³ s⁻¹, S₀ = 0.498 μm⁻², β = 0.4 s⁻¹, τ = 0.5 s, t₀ = 10 s, and R = 2.75 μm. (D) The dependence of the full-engulfment time on the ligand density, ρ_L, showing a minimum at intermediate ρ_L. Parameters as in panel C. Additional parameters are ρ₀ = 50 μm⁻², $\mathcal{E}$ = 3, $\mathcal{B}$ = 20, D_S = 1 μm² s⁻¹, and L = 50 μm. To see this figure in color, go online.

Figure 7

Comparison of oblate and prolate spheroids. (A) Sketch of the two spheroids, parameterized by R₁ and R₂. For oblate spheroids (R₁ > R_2.), the lowest curvature region is the first to be engulfed, whereas for prolate spheroids (R₁ < R_2.), the highest curvature region is engulfed first. (B) Progression of engulfment with time. (Red) Oblate spheroid with R₁ = R₂ = 4.1 μm and R₃ = 0.62 μm. (Blue) Prolate spheroid with R₁ = R₂ = 0.87 μm and R₃ = 4 μm. (Solid lines) Full model with signaling; (dashed lines) pure diffusion model without signaling. (Solid circles) Half- and full engulfment. (Numbers) Order of engulfment. To see this figure in color, go online.