A model for sigma factor competition in bacterial cells

Abstract

Sigma factors control global switches of the genetic expression program in bacteria. Different sigma factors compete for binding to a limited pool of RNA polymerase (RNAP) core enzymes, providing a mechanism for cross-talk between genes or gene classes via the sharing of expression machinery. To analyze the contribution of sigma factor competition to global changes in gene expression, we develop a theoretical model that describes binding between sigma factors and core RNAP, transcription, non-specific binding to DNA and the modulation of the availability of the molecular components. The model is validated by comparison with in vitro competition experiments, with which excellent agreement is found. Transcription is affected via the modulation of the concentrations of the different types of holoenzymes, so saturated promoters are only weakly affected by sigma factor competition. However, in case of overlapping promoters or promoters recognized by two types of sigma factors, we find that even saturated promoters are strongly affected. Active transcription effectively lowers the affinity between the sigma factor driving it and the core RNAP, resulting in complex cross-talk effects. Sigma factor competition is not strongly affected by non-specific binding of core RNAPs, sigma factors and holoenzymes to DNA. Finally, we analyze the role of increased core RNAP availability upon the shut-down of ribosomal RNA transcription during the stringent response. We find that passive up-regulation of alternative sigma-dependent transcription is not only possible, but also displays hypersensitivity based on the sigma factor competition. Our theoretical analysis thus provides support for a significant role of passive control during that global switch of the gene expression program.

Figure 1. Model for sigma factor competition.

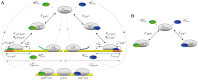
(A) Model for sigma factor competition with two types of sigma factors, the housekeeping sigma factor and a generic alternative sigma factor : the model describes binding of or to core RNA polymerase () to form holoenzymes ( and ) as well as transcription (promoter binding, transcription initiation and elongation) of the cognate genes and non-specific binding of holoenzymes and core RNAPs to DNA. (B) Core model for holoenzyme formation.

Figure 2. Holoenzyme formation.

(A) Number of holoenzymes and as a function of the copy number of alternative sigma factors. Quantities of all molecular species are expressed as absolute numbers per cell. The gray dashed line represents the onset of the competition, when . The values of the parameters used in the simulations are summarized in Table 1. (B) Determination of the sigma-core dissociation constants for and (see Table 2) by fitting the results of binding assays between cores and sigma factors , . The number of core-sigma complexes normalized to the maximal number of holoenzymes, . Stars show the experimental data and lines are due to the fit. (C) Comparison of model predictions (lines) with an in vitro competition experiment with a fixed amount of core and different equimolar amounts of and (stars) in the same conditions as in (B). The plot shows the fraction of sigma factors bound in holoenzymes as a function of the total sigma factor concentration, .

Figure 3. Transcription rate.

(A) Normalized transcription rate (Equation 12) for a σ ⁷⁰-dependent promoter as a function of the number of alternative sigma factors. The numbers of and cores are fixed. The blue line is for a saturated promoter (with M) and the cyan line for an unsaturated promoter (with M). (B) Comparison of model predictions (lines) with an in vitro competition experiment with a fixed amount of core and σ^H and different amounts of (stars). The plot shows the transcription rate of a σ^H-dependent gene (normalized to the maximal value) as a function of the concentration . (C) The sigma-core and the holoenzyme-promoter dissociation constants (see Table 2) are determined by fitting the results of transcription rate experiments with a fixed amount of cores in the same conditions as in (B) without competition in the presence of a DNA template containing σ^H- and σ ⁷⁰-driven genes , . (D) When a σ ⁷⁰-dependent promoter also binds another type of holoenzyme or overlaps to another promoter, also acts as a repressor of the σ ⁷⁰-dependent transcription. (E) Normalized transcription rate of a saturated and unsaturated σ ⁷⁰-dependent promoter as a function of the number of (blue and cyan solid lines with M and M, respectively). The dashed line show the corresponding results in the absence of repression by promoter sharing or overlapping.

Figure 4. Effect of non-specific binding of holoenzymes and cores to DNA.

(A) Formation of holoenzymes in the presence of one type of sigma factor in the absence of DNA (no non-specific binding, dashed line), in the presence of DNA with equal non-specific binding affinities of cores and holoenzymes ( M, dotted line) and with different non-specific binding affinities ( M, M, solid line). (B) Number of free cytoplasmic holoenzymes and (upper row) and total number of holoenzymes (free and non-specifically bound, , lower row) as functions of the copy number of alternative sigma factors for three different combinations of non-specific binding affinities: in (i) and (ii) all non-specific dissociation constant are equal ( M), in (iii) and (iv) the non-specific dissociation constant for the core is smaller than for the holoenzymes ( M, M), in (v) and (vi) the non-specific dissociation constant for the is smaller than for and core ( M, M). The dashed lines in all panels shows the reference case without DNA (no non-specific binding).

Figure 5. Effect of transcript elongation.

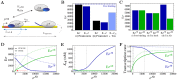
(A) Active elongation sequesters core RNAPs for the length of the operon and sigma subunit for some nucleotides. (B) Formation of holoenzymes in the presence of one type of sigma factor without DNA (no specific binding and no transcription with nM, dashed line), in the presence of specific binding (holoenzymes bind to promoter with M but do not transcribe, case (i)) and in the presence of both specific binding and transcription (case (ii)). The black bars () show the case when sigma factor and core unbind as holoenzyme (the binding affinity is described by the equilibrium dissociation constant), the dark blue () and the light blue bars () when sigma factor separates from core either after promoter unbinding or gene transcription and after 300 nucleotides, respectively (thus, the binding affinity is ). (C) Number of holoenzymes and as a function of the copy number of alternative sigma factors in the absence of DNA (case (i)), with transcription of both σ ⁷⁰- and σ^Alt-dependent genes but with unbinding of sigma factor after 300 nucleotides and core at the end of the operon (case (ii)) and only with the transcription of the σ^Alt-dependent genes (case (iii)). Values of the parameters are the same as in Figure 5B. (D) Formation of holoenzymes and as a function of the copy number of alternative sigma factors without DNA (dashed lines) and transcript elongation (solid lines). (E) Modulation of the effective binding affinities by sigma factor competition related to the case of Figure 5D. (F) Normalized transcription rate for σ ⁷⁰- and σ^Alt-dependent promoters as a function of the number of alternative sigma factors, related to the case of Figure 5D (with nM and nM).

Figure 6. Stringent response.

(A) During the stringent response RNA polymerases involved in rRNA transcription are quickly released to increase the pool of free cores. (B) Number of holoenzymes and as a function of the copy number of core RNAPs. The black dashed lines show the number of available RNAPs during the exponential growth state () and during the stringent response state. The gray region shows the range of core RNAP for which there is sigma factor competition. (C) Response factor of the alternative sigma factor-dependent gene transcription (with M) to an increase of concentration of RNAPs. The blue dashed line shows the maximal sensitivity, that for strong core-sigma binding, is found for and lies in the competition region. (D) Number of alternative holoenzymes and (E) response factor related to the σ^Alt-dependent gene transcription as a function of the number of core RNAPs and alternative sigma factors (with M). The white line encloses the region of sigma factor competition. The points show possible values of cores and alternative sigma factors for a cell in the exponential growth state and in the stringent state.