Learning To Fold Proteins Using Energy Landscape Theory
- PMID: 25308991
- PMCID: PMC4189132
- DOI: 10.1002/ijch.201300145
Learning To Fold Proteins Using Energy Landscape Theory
Abstract
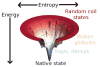
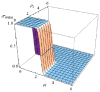
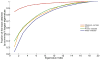
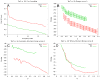
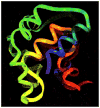
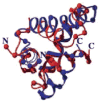
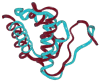
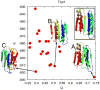
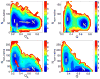
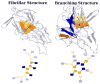
This review is a tutorial for scientists interested in the problem of protein structure prediction, particularly those interested in using coarse-grained molecular dynamics models that are optimized using lessons learned from the energy landscape theory of protein folding. We also present a review of the results of the AMH/AMC/AMW/AWSEM family of coarse-grained molecular dynamics protein folding models to illustrate the points covered in the first part of the article. Accurate coarse-grained structure prediction models can be used to investigate a wide range of conceptual and mechanistic issues outside of protein structure prediction; specifically, the paper concludes by reviewing how AWSEM has in recent years been able to elucidate questions related to the unusual kinetic behavior of artificially designed proteins, multidomain protein misfolding, and the initial stages of protein aggregation.
Figures

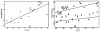






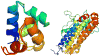



References
-
- Anfinsen C. Studies of the principles that govern the folding of protein chains (nobel lecture) Norstedt & Sons; Stockholm: 1972. - PubMed
-
- Baker D, Agard DA. Kinetics versus thermodynamics in protein folding. Biochemistry. 1994;33(24):7505–7509. - PubMed
-
- Benilova I, Karran E, De Strooper B. The toxic a-beta oligomer and alzheimer’s disease: an emperor in need of clothes. Nature neuroscience. 2012;15(3):349–357. - PubMed
-
- Bennett MJ, Sawaya MR, Eisenberg D. Deposition diseases and 3d domain swapping. Structure. 2006;14(5):811–824. - PubMed
-
- Berthelot K, Cullin C, Lecomte S. What does make an amyloid toxic: Morphology, structure or interaction with membrane? Biochimie. 2012:12–19. - PubMed
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
