The power of coarse graining in biomolecular simulations
- PMID: 25309628
- PMCID: PMC4171755
- DOI: 10.1002/wcms.1169
The power of coarse graining in biomolecular simulations
Abstract
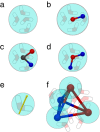
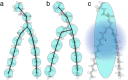
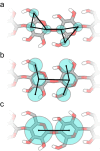
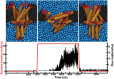
Computational modeling of biological systems is challenging because of the multitude of spatial and temporal scales involved. Replacing atomistic detail with lower resolution, coarse grained (CG), beads has opened the way to simulate large-scale biomolecular processes on time scales inaccessible to all-atom models. We provide an overview of some of the more popular CG models used in biomolecular applications to date, focusing on models that retain chemical specificity. A few state-of-the-art examples of protein folding, membrane protein gating and self-assembly, DNA hybridization, and modeling of carbohydrate fibers are used to illustrate the power and diversity of current CG modeling.
Figures


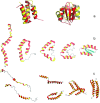

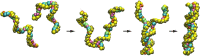

References
-
- Dror RO, Dirks RM, Grossman JP, Xu H, Shaw DE. Biomolecular simulation: a computational microscope for molecular biology. Annu Rev Biophys. 2012;41:429–452. - PubMed
-
- Voth GA. Coarse-Graining of Condensed Phase and Biomolecular Systems. Boca Raton, FL: CRC Press, Taylor and Francis; 2009.
-
- Bond PJ, Holyoake J, Ivetac A, Khalid S, Sansom MSP. Coarse-grained molecular dynamics simulations of membrane proteins and peptides. J Struct Biol. 2007;157:593–605. - PubMed
-
- Lyubartsev AP, Laaksonen A. Calculation of effective interaction potentials from radial distribution functions: a reverse Monte Carlo approach. Phys Rev E. 1995;52:3730. - PubMed
LinkOut - more resources
Full Text Sources
Other Literature Sources
