Quantitative technique for robust and noise-tolerant speed measurements based on speckle decorrelation in optical coherence tomography
- PMID: 25322018
- PMCID: PMC4247190
- DOI: 10.1364/OE.22.024411
Quantitative technique for robust and noise-tolerant speed measurements based on speckle decorrelation in optical coherence tomography
Abstract
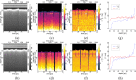
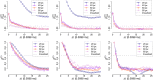
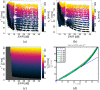
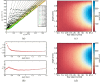
Intensity-based techniques in optical coherence tomography (OCT), such as those based on speckle decorrelation, have attracted great interest for biomedical and industrial applications requiring speed or flow information. In this work we present a rigorous analysis of the effects of noise on speckle decorrelation, demonstrate that these effects frustrate accurate speed quantitation, and propose new techniques that achieve quantitative and repeatable measurements. First, we derive the effect of background noise on the speckle autocorrelation function, finding two detrimental effects of noise. We propose a new autocorrelation function that is immune to the main effect of background noise and permits quantitative measurements at high and moderate signal-to-noise ratios. At the same time, this autocorrelation function is able to provide motion contrast information that accurately identifies areas with movement, similar to speckle variance techniques. In order to extend the SNR range, we quantify and model the second effect of background noise on the autocorrelation function through a calibration. By obtaining an explicit expression for the decorrelation time as a function of speed and diffusion, we show how to use our autocorrelation function and noise calibration to measure a flowing liquid. We obtain accurate results, which are validated by Doppler OCT, and demonstrate a very high dynamic range (> 600 mm/s) compared to that of Doppler OCT (±25 mm/s). We also derive the behavior for low flows, and show that there is an inherent non-linearity in speed measurements in the presence of diffusion due to statistical fluctuations of speckle. Our technique allows quantitative and robust measurements of speeds using OCT, and this work delimits precisely the conditions in which it is accurate.
Figures



Similar articles
-
Signal-carrying speckle in optical coherence tomography: a methodological review on biomedical applications.J Biomed Opt. 2022 Mar;27(3):030901. doi: 10.1117/1.JBO.27.3.030901. J Biomed Opt. 2022. PMID: 35289154 Free PMC article.
-
Comparison of Kasai autocorrelation and maximum likelihood estimators for Doppler optical coherence tomography.IEEE Trans Med Imaging. 2013 Jun;32(6):1033-42. doi: 10.1109/TMI.2013.2248163. Epub 2013 Feb 21. IEEE Trans Med Imaging. 2013. PMID: 23446044 Free PMC article.
-
Maximum likelihood Doppler frequency estimation under decorrelation noise for quantifying flow in optical coherence tomography.IEEE Trans Med Imaging. 2014 Jun;33(6):1313-23. doi: 10.1109/TMI.2014.2309986. Epub 2014 Mar 11. IEEE Trans Med Imaging. 2014. PMID: 24760902
-
Noise and bias in optical coherence tomography intensity signal decorrelation.OSA Contin. 2020 Apr 15;3(4):709-741. doi: 10.1364/OSAC.385431. Epub 2020 Mar 17. OSA Contin. 2020. PMID: 34085035 Free PMC article.
-
Growing Trend to Adopt Speckle Variance Optical Coherence Tomography for Biological Tissue Assessments in Pre-Clinical Applications.Micromachines (Basel). 2024 Apr 25;15(5):564. doi: 10.3390/mi15050564. Micromachines (Basel). 2024. PMID: 38793137 Free PMC article. Review.
Cited by
-
A Neural Network Approach to Quantify Blood Flow from Retinal OCT Intensity Time-Series Measurements.Sci Rep. 2020 Jun 15;10(1):9611. doi: 10.1038/s41598-020-66158-8. Sci Rep. 2020. PMID: 32541887 Free PMC article.
-
Enhanced microvascular imaging through deep learning-driven OCTA reconstruction with squeeze-and-excitation block integration.Biomed Opt Express. 2024 Sep 3;15(10):5592-5608. doi: 10.1364/BOE.525928. eCollection 2024 Oct 1. Biomed Opt Express. 2024. PMID: 39421773 Free PMC article.
-
Signal-carrying speckle in optical coherence tomography: a methodological review on biomedical applications.J Biomed Opt. 2022 Mar;27(3):030901. doi: 10.1117/1.JBO.27.3.030901. J Biomed Opt. 2022. PMID: 35289154 Free PMC article.
-
Laminar microvascular transit time distribution in the mouse somatosensory cortex revealed by Dynamic Contrast Optical Coherence Tomography.Neuroimage. 2016 Jan 15;125:350-362. doi: 10.1016/j.neuroimage.2015.10.017. Epub 2015 Oct 20. Neuroimage. 2016. PMID: 26477654 Free PMC article.
-
Real-time co-localized OCT surveillance of laser therapy using motion corrected speckle decorrelation.Biomed Opt Express. 2020 May 7;11(6):2925-2950. doi: 10.1364/BOE.385654. eCollection 2020 Jun 1. Biomed Opt Express. 2020. PMID: 32637233 Free PMC article.
References
-
- Bouma B. E., Tearney G. J., eds., Handbook of optical coherence tomography (Marcel Dekker Inc, 2002).
-
- Stifter D., Leiss-Holzinger E., Major Z., Baumann B., Pircher M., Götzinger E., Hitzenberger C. K., Heise B., “Dynamic optical studies in materials testing with spectral-domain polarization-sensitive optical coherence tomography,” Opt. Express 18, 25712–25725 (2010).10.1364/OE.18.025712 - DOI - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

