Cooling a band insulator with a metal: fermionic superfluid in a dimerized holographic lattice
- PMID: 25324029
- PMCID: PMC4200405
- DOI: 10.1038/srep06655
Cooling a band insulator with a metal: fermionic superfluid in a dimerized holographic lattice
Abstract
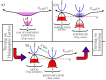
A cold atomic realization of a quantum correlated state of many fermions on a lattice, eg. superfluid, has eluded experimental realization due to the entropy problem. Here we propose a route to realize such a state using holographic lattice and confining potentials. The potentials are designed to produces a band insulating state (low heat capacity) at the trap center, and a metallic state (high heat capacity) at the periphery. The metal "cools" the central band insulator by extracting out the excess entropy. The central band insulator can be turned into a superfluid by tuning an attractive interaction between the fermions. Crucially, the holographic lattice allows the emergent superfluid to have a high transition temperature - even twice that of the effective trap temperature. The scheme provides a promising route to a laboratory realization of a fermionic lattice superfluid, even while being adaptable to simulate other many body states.
Figures
 ,
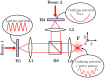
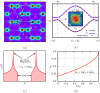
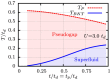
,  are lattice basis vectors. The distances a, b, c can be chosen by a suitable design of the hologram to obtain desired values of t/td and tp/td. (b) Conduction(C) and valence(V) band dispersions showing the energy gap; blue(C) and black(V) bands correspond to that shown in fig. 1(b). The gap occurs at ±k0 along k1 = k2, as shown by the dashed line in the Brillouin zone plot(inset) of εC − εV (see equation (3)). Holographic lattice parameter values are V/ER = 5.0, w/a = 0.3 and b/a = 1.04. The area around ±k0 is highlighted with lighter contours. The resulting tight binding model has t/td = tp/td = 0.64. (c) One particle density of states around the band gap, showing the van Hove singularities. (d) Dependence of wavevector k0 (at which peaks in time-of-flight images are expected) on t/td.
are lattice basis vectors. The distances a, b, c can be chosen by a suitable design of the hologram to obtain desired values of t/td and tp/td. (b) Conduction(C) and valence(V) band dispersions showing the energy gap; blue(C) and black(V) bands correspond to that shown in fig. 1(b). The gap occurs at ±k0 along k1 = k2, as shown by the dashed line in the Brillouin zone plot(inset) of εC − εV (see equation (3)). Holographic lattice parameter values are V/ER = 5.0, w/a = 0.3 and b/a = 1.04. The area around ±k0 is highlighted with lighter contours. The resulting tight binding model has t/td = tp/td = 0.64. (c) One particle density of states around the band gap, showing the van Hove singularities. (d) Dependence of wavevector k0 (at which peaks in time-of-flight images are expected) on t/td.  ,
,  are reciprocal lattice vectors.
are reciprocal lattice vectors.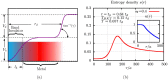
References
-
- Cirac J. I. & Zoller P. Goals and opportunities in quantum simulation. Nat. Phys. 8, 264 (2012).
-
- Trabesinger A. Quantum simulation. Nat. Phys. 8, 263 (2012).
-
- Lee P. A., Nagaosa N. & Wen X.-G. Doping a mott insulator: Physics of high-temperature superconductivity. Rev. Mod. Phys. 78, 17 (2006).
-
- Nayak C., Simon S. H., Stern A., Freedman M. & Das Sarma S. Non-abelian anyons and topological quantum computation. Rev. Mod. Phys. 80, 1083 (2008).
-
- Lin Y.-J. et al. Bose-einstein condensate in a uniform light-induced vector potential. Phys. Rev. Lett. 102, 130401 (2009). - PubMed
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources

