Structured chaos shapes spike-response noise entropy in balanced neural networks
- PMID: 25324772
- PMCID: PMC4183092
- DOI: 10.3389/fncom.2014.00123
Structured chaos shapes spike-response noise entropy in balanced neural networks
Abstract
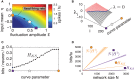
Large networks of sparsely coupled, excitatory and inhibitory cells occur throughout the brain. For many models of these networks, a striking feature is that their dynamics are chaotic and thus, are sensitive to small perturbations. How does this chaos manifest in the neural code? Specifically, how variable are the spike patterns that such a network produces in response to an input signal? To answer this, we derive a bound for a general measure of variability-spike-train entropy. This leads to important insights on the variability of multi-cell spike pattern distributions in large recurrent networks of spiking neurons responding to fluctuating inputs. The analysis is based on results from random dynamical systems theory and is complemented by detailed numerical simulations. We find that the spike pattern entropy is an order of magnitude lower than what would be extrapolated from single cells. This holds despite the fact that network coupling becomes vanishingly sparse as network size grows-a phenomenon that depends on "extensive chaos," as previously discovered for balanced networks without stimulus drive. Moreover, we show how spike pattern entropy is controlled by temporal features of the inputs. Our findings provide insight into how neural networks may encode stimuli in the presence of inherently chaotic dynamics.
Keywords: chaotic networks; network dynamics; neural excitability; neural variability; spiking stimulus responses.
Figures
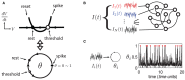



Similar articles
-
Encoding in Balanced Networks: Revisiting Spike Patterns and Chaos in Stimulus-Driven Systems.PLoS Comput Biol. 2016 Dec 14;12(12):e1005258. doi: 10.1371/journal.pcbi.1005258. eCollection 2016 Dec. PLoS Comput Biol. 2016. PMID: 27973557 Free PMC article.
-
Dynamical entropy production in spiking neuron networks in the balanced state.Phys Rev Lett. 2010 Dec 31;105(26):268104. doi: 10.1103/PhysRevLett.105.268104. Epub 2010 Dec 30. Phys Rev Lett. 2010. PMID: 21231716
-
How Chaotic is the Balanced State?Front Comput Neurosci. 2009 Nov 10;3:13. doi: 10.3389/neuro.10.013.2009. eCollection 2009. Front Comput Neurosci. 2009. PMID: 19936316 Free PMC article.
-
Is there chaos in the brain? II. Experimental evidence and related models.C R Biol. 2003 Sep;326(9):787-840. doi: 10.1016/j.crvi.2003.09.011. C R Biol. 2003. PMID: 14694754 Review.
-
Chaotic recurrent neural networks for brain modelling: A review.Neural Netw. 2025 Apr;184:107079. doi: 10.1016/j.neunet.2024.107079. Epub 2024 Dec 27. Neural Netw. 2025. PMID: 39756119 Review.
Cited by
-
Commentary on Structured chaos shapes spike-response noise entropy in balanced neural networks, by Lajoie, Thivierge, and Shea-Brown.Front Comput Neurosci. 2015 Mar 10;9:23. doi: 10.3389/fncom.2015.00023. eCollection 2015. Front Comput Neurosci. 2015. PMID: 25805988 Free PMC article. No abstract available.
-
Dynamic Recovery: GABA Agonism Restores Neural Variability in Older, Poorer Performing Adults.J Neurosci. 2021 Nov 10;41(45):9350-9360. doi: 10.1523/JNEUROSCI.0335-21.2021. Epub 2021 Nov 3. J Neurosci. 2021. PMID: 34732523 Free PMC article. Clinical Trial.
-
Encoding in Balanced Networks: Revisiting Spike Patterns and Chaos in Stimulus-Driven Systems.PLoS Comput Biol. 2016 Dec 14;12(12):e1005258. doi: 10.1371/journal.pcbi.1005258. eCollection 2016 Dec. PLoS Comput Biol. 2016. PMID: 27973557 Free PMC article.
References
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

