. 2014 Jun 26;4(2):109-22.

doi: 10.5662/wjm.v4.i2.109.

Choosing inclusion criteria that minimize the time and cost of clinical trials

Charles F Babbs¹

Affiliations

PMID: 25332910
PMCID: PMC4202479
DOI: 10.5662/wjm.v4.i2.109

Choosing inclusion criteria that minimize the time and cost of clinical trials

Charles F Babbs. World J Methodol. 2014.

. 2014 Jun 26;4(2):109-22.

doi: 10.5662/wjm.v4.i2.109.

Author

Charles F Babbs¹

Affiliation

¹ Charles F Babbs, Weldon School of Biomedical Engineering, Purdue University, West Lafayette, IN 47907, United States.

PMID: 25332910
PMCID: PMC4202479
DOI: 10.5662/wjm.v4.i2.109

Abstract

Aim: To present statistical tools to model and optimize the cost of a randomized clinical trial as a function of the stringency of patient inclusion criteria.

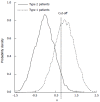
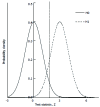
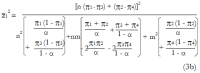
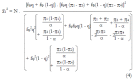
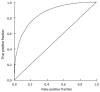
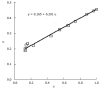
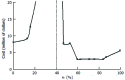
Methods: We consider a two treatment, dichotomous outcome trial that includes a proportion of patients who are strong responders to the tested intervention. Patients are screened for inclusion using an arbitrary number of test results that are combined into an aggregate suitability score. The screening score is regarded as a diagnostic test for the responsive phenotype, having a specific cutoff value for inclusion and a particular sensitivity and specificity. The cutoff is a measure of stringency of inclusion criteria. Total cost is modeled as a function of the cutoff value, number of patients screened, the number of patients included, the case occurrence rate, response probabilities for control and experimental treatments, and the trial duration required to produce a statistically significant result with a specified power. Regression methods are developed to estimate relevant model parameters from pilot data in an adaptive trial design.

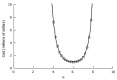
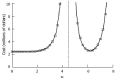
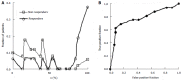
Results: The patient numbers and total cost are strongly related to the choice of the cutoff for inclusion. Clear cost minimums exist between 5.6 and 6.1 on a representative 10-point scale of exclusiveness. Potential cost savings for typical trial scenarios range in millions of dollars. As the response rate for controls approaches 50%, the proper choice of inclusion criteria can mean the difference between a successful trial and a failed trial.

Conclusion: Early formal estimation of optimal inclusion criteria allows planning of clinical trials to avoid high costs, excessive delays, and moral hazards of Type II errors.

Keywords: Adaptive trial designs; Biomarkers; Clinical trials; Device; Drug therapy; Ethics; Methodology; Optimal allocation; Personalized medicine; Sequential design.

PubMed Disclaimer

Figures

**Figure 1**
Separation of patient response phenotypes to a tested treatment according to an aggregate predictive variable, x. The fraction of type 1 responders to the right of the cutoff is the true positive fraction. The fraction of type 2 non-responders to the right of the cutoff is the false positive fraction. In this general example the units of x are arbitrary.

**Figure 2**
Calculation of power from probability density distributions for the null hypothesis (H0) and for an alternative hypothesis (H1). The dashed line shows critical value for significance (1.96 for two-tailed P < 0.05). The area under the thick curve to the right of the critical value is the statistical power of the test of H0.

**Figure 3**
A sample receiver operating characteristic curve for a hypothetical screening test. In this example type 1 patients had screening scores, x, with a mean of 5.5 and a standard deviation of 1; type 2 patients had screening scores, x, with a mean of 4 and a standard deviation of 1. As the cutoff value xc is swept from 1.0 toward zero, a family of true positive and false positive fractions is created to generate the receiver operating characteristic (ROC) curve.

**Figure 4**
Numbers of patients screened and enrolled in a model study of heterogeneous responders having a statistically significant positive result. For this model the proportion of type 1, good responders q = 0.2, the response probability for type 1 patients, π₁ = 1.0, the response probability for type 2, poor responders, π₂ = 0. The response probabilities for both phenotypes to the control treatment, π₃ and π₄ both equal 0.2. The mean value of the z statistic for the alternative hypothesis is 2.96 (84% power for the trial). The proportion of patients, α, assigned to the experimental group is 0.5.

**Figure 5**
Cost estimates in a model study of heterogeneous responders. Cost constants in thousands of dollars are as follows: screening cost per case c₁ = 1, treatment cost c₂ = 10, opportunity cost c₃ = 100/yr, case rate r = 50/yr, follow up time t =1 yr. Other details as in Figure 4.

**Figure 6**
Cost estimates in a scenario with good responsiveness to the control treatment in patients who are non-responsive to the experimental treatment. π₁ = 1.0, π₂ = 0, π₃ = π₄ = 0.4. Other details as in Figure 5. Dashed line divides the x-domain into regions of a significant negative effect (to the left) vs a significant positive effect (right). Near x_c = 4.4 the cost of disproving the null hypothesis when it is exactly true becomes infinite.

**Figure 7**
Fraction of patients. A: Separation of observed responders and non-responders to the experimental treatment along the x-domain in this reconstructed preliminary study. The fraction of patients with each x-value is show on the vertical axis. Patients with x-scores over 60% have a much greater likelihood of responding; B: ROC curve for the screening procedure.

**Figure 8**
Regression analysis on the last two columns of Table 3. A plot of the hybrid variable, y = pC(u)(π + u), vs u can be used to evaluate model parameters π₃ and π₄. The slope of the regression line is π₄, and the intercept divided by π is π₃.

**Figure 9**
Cost estimates in a realistic test data set for targeted drug therapy of lung cancer, presented in Tables 2 and 3. Cost constants in thousands of dollars are as follows: screening cost per case c1 = 1, treatment cost c₂ = 10, opportunity cost c₃ = 100/year, case rate r = 50/year, follow up time t =1 year. Cost to the right of the dashed vertical asymptote are for a significant positive result (experimental treatment better than control). Costs to the left of the dashed vertical asymptote are for a significant negative result (experimental treatment worse than control).

See this image and copyright information in PMC

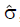
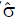
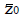
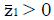
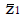
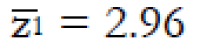
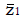
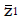
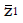
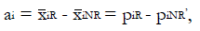
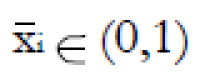
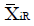
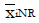
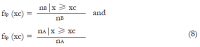
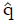
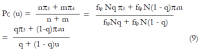
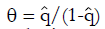
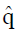
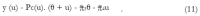
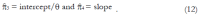
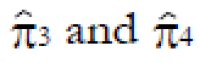
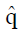
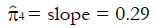
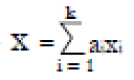
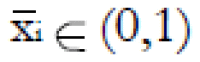
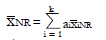
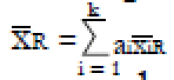
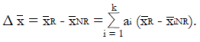
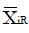
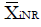
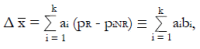
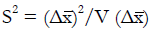
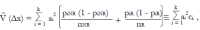
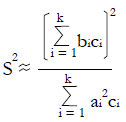
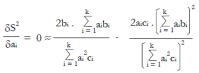
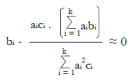
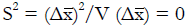
References

1. Anderson JE, Hansen LL, Mooren FC, Post M, Hug H, Zuse A, Los M. Methods and biomarkers for the diagnosis and prognosis of cancer and other diseases: towards personalized medicine. Drug Resist Updat. 2006;9:198–210. - PubMed
1. Ross JS, Slodkowska EA, Symmans WF, Pusztai L, Ravdin PM, Hortobagyi GN. The HER-2 receptor and breast cancer: ten years of targeted anti-HER-2 therapy and personalized medicine. Oncologist. 2009;14:320–368. - PubMed
1. van’t Veer LJ, Bernards R. Enabling personalized cancer medicine through analysis of gene-expression patterns. Nature. 2008;452:564–570. - PubMed
1. Yao Q, Wei LJ. Play the winner for phase II/III clinical trials. Stat Med. 1996;15:2413–223; discussion 2413-223;. - PubMed
1. Bauer P, Köhne K. Evaluation of experiments with adaptive interim analyses. Biometrics. 1994;50:1029–1041. - PubMed

LinkOut - more resources

Full Text Sources
Other Literature Sources
- scite Smart Citations
Research Materials
- NCI CPTC Antibody Characterization Program

Save citation to file

Email citation

Add to Collections

Add to My Bibliography

Your saved search

Create a file for external citation management software

Your RSS Feed

Choosing inclusion criteria that minimize the time and cost of clinical trials

Affiliation

Choosing inclusion criteria that minimize the time and cost of clinical trials

Author

Affiliation

Abstract

Figures

References

LinkOut - more resources

Full Text Sources

Other Literature Sources

Research Materials