The diffusion model is not a deterministic growth model: comment on Jones and Dzhafarov (2014)

Abstract

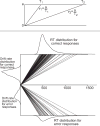
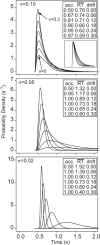
Jones and Dzhafarov (2014) claim that several current models of speeded decision making in cognitive tasks, including the diffusion model, can be viewed as special cases of other general models or model classes. The general models can be made to match any set of response time (RT) distribution and accuracy data exactly by a suitable choice of parameters and so are unfalsifiable. The implication of their claim is that models like the diffusion model are empirically testable only by artificially restricting them to exclude unfalsifiable instances of the general model. We show that Jones and Dzhafarov's argument depends on enlarging the class of "diffusion" models to include models in which there is little or no diffusion. The unfalsifiable models are deterministic or near-deterministic growth models, from which the effects of within-trial variability have been removed or in which they are constrained to be negligible. These models attribute most or all of the variability in RT and accuracy to across-trial variability in the rate of evidence growth, which is permitted to be distributed arbitrarily and to vary freely across experimental conditions. In contrast, in the standard diffusion model, within-trial variability in evidence is the primary determinant of variability in RT. Across-trial variability, which determines the relative speed of correct responses and errors, is theoretically and empirically constrained. Jones and Dzhafarov's attempt to include the diffusion model in a class of models that also includes deterministic growth models misrepresents and trivializes it and conveys a misleading picture of cognitive decision-making research. (PsycINFO Database Record (c) 2014 APA, all rights reserved).

Figure 1

The top panel illustrates the deterministic growth model of Equation 1, including the one-to-one correspondence between time and velocity (drift rate). The distribution of velocities is fixed by the distribution of times because each time, T₁ and T₂, is uniquely associated with a particular velocity, v₁ and v₂. The bottom panel shows an example of correct and error response time (RT) distributions generated by the standard diffusion model (horizontal axes) and the distribution of drift rates in the deterministic model needed to produce them (vertical axis). The parameters of the diffusion model used to generate the simulated RT distributions were a = 0.12, T_er = 0.4, z = 0.06, η = 0.12, s_z = 0.02, s_t = 0.1, and v = 0.2.

Figure 2

Examples of the drift rate distributions for the deterministic model derived from response time (RT) distributions for the diffusion model. The drift rates for the diffusion model were 0.0, 0.2, and 0.4; the other parameters were the same as in Figure 1. The positive lobes of the drift rate distributions describe the distributions of correct responses and the negative lobes describe the distributions of errors. The proportions of probability mass in the positive lobes are the proportions of correct responses. Separate drift rate distributions, with different shapes and different proportions of mass in their positive and negative lobes, are needed for each value of drift rate.

Figure 3

Examples of response time (RT) distributions for correct responses for the standard diffusion model as a function of drift rate (varying from 0 to 0.3 in steps of 0.06) and as a function of the infinitesimal standard deviation (σ = 0.10, 0.05, and 0.02 for the top, middle, and bottom panels, respectively). The inset in the top panel shows the distributions scaled to the same peak value for σ = 0.10. The inset tables show values of accuracy (acc.) and mean RT as a function of drift rate. Only for σ = 0.10 do processes with drift rate greater than zero produce a non-negligible proportion of errors.