Humans use directed and random exploration to solve the explore-exploit dilemma

Abstract

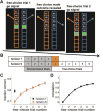
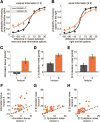
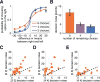
All adaptive organisms face the fundamental tradeoff between pursuing a known reward (exploitation) and sampling lesser-known options in search of something better (exploration). Theory suggests at least two strategies for solving this dilemma: a directed strategy in which choices are explicitly biased toward information seeking, and a random strategy in which decision noise leads to exploration by chance. In this work we investigated the extent to which humans use these two strategies. In our "Horizon task," participants made explore-exploit decisions in two contexts that differed in the number of choices that they would make in the future (the time horizon). Participants were allowed to make either a single choice in each game (horizon 1), or 6 sequential choices (horizon 6), giving them more opportunity to explore. By modeling the behavior in these two conditions, we were able to measure exploration-related changes in decision making and quantify the contributions of the two strategies to behavior. We found that participants were more information seeking and had higher decision noise with the longer horizon, suggesting that humans use both strategies to solve the exploration-exploitation dilemma. We thus conclude that both information seeking and choice variability can be controlled and put to use in the service of exploration.

Figure 1

Task design (A). Example screen shots from a horizon 6 game showing the first free-choice trial, the result of the choice (after it is made), and the start of the second free-choice trial (B). Schematic showing the different trial types in the two horizon conditions. Each game began with four forced-choice trials before one or a sequence of six free-choice trials. In all conditions, the first free-choice trial (orange) was the main focus of subsequent analyses (C). Learning curves showing the fraction of times the correct option (i.e., the option with the higher generative mean) was chosen as a function of free-choice trial number for the different horizon conditions. This demonstrates that participants performed at above-chance levels and improved as the game progressed (D). Correlation between the difference in observed means of each option and the difference in the number of times each option has been played as a function of free-choice trial number. Only the very first trial showed an absence of correlation; thereafter, there was a strong correlation as participants received more information about the more rewarding options that they selected. See the online article for the color version of this figure.

Figure 2

Behavior on the first free-choice trial. Choice curves for the unequal (A) and equal (B) information conditions. Filled circles = experimental data; solid lines = average over participants of model-derived choice curves (A). These curves show the fraction of times the more informative option was chosen on the first free-choice trial as a function of the difference in mean between the more informative option and the less informative option. As the horizon increased, the more informative option was chosen more often, indicating an information bonus. In addition, the slope of the curves decreased, indicating a change in decision noise (B). In the equal condition, as the horizon increased there was no change in indifference point because both options were equally informative. The slope of the curves, however, decreased again, consistent with an increase in decision noise with horizon. Mean parameter fits for the information bonus (C) and decision noise in the [1 3] condition (D) and decision noise in the [2 2] condition (E) showing an increase in information bonus and decision noise between horizons 1 and 6. Error bars are s.e.m. across participants. Scatter plots comparing parameter fits for individual subjects in horizon 1 and horizon 6. The dashed lines denote equality. This shows that the increase in information bonus (F) and decision noise (G and H) with horizon holds for almost all of the subjects. See the online article for the color version of this figure.

Figure 3

Change in decision noise across the horizon 6 game (A). Choice curves for the equal information conditions on the first [2 2], third [3 3] and fifth [4 4] free-choice trials in horizon 6 games. This shows an increase in slope on the later trials relative to the first trial consistent with a decrease in random exploration (B). Participants’ mean decision noise extracted from the model fits showing a decrease in decision noise in the equal conditions over the horizon 6 games (C, D, E). Comparison between the individual participants’ decision noise in the three information conditions shows that the decrease in decision noise between the first and later trials holds for most subjects (C) and (D), whereas there is no difference between the decision noise in the [3 3] and [4 4] conditions (E). See the online article for the color version of this figure.