Magnetic thin-film insulator with ultra-low spin wave damping for coherent nanomagnonics

Abstract

Wave control in the solid state has opened new avenues in modern information technology. Surface-acoustic-wave-based devices are found as mass market products in 100 millions of cellular phones. Spin waves (magnons) would offer a boost in today's data handling and security implementations, i.e., image processing and speech recognition. However, nanomagnonic devices realized so far suffer from the relatively short damping length in the metallic ferromagnets amounting to a few 10 micrometers typically. Here we demonstrate that nm-thick YIG films overcome the damping chasm. Using a conventional coplanar waveguide we excite a large series of short-wavelength spin waves (SWs). From the data we estimate a macroscopic of damping length of about 600 micrometers. The intrinsic damping parameter suggests even a record value about 1 mm allowing for magnonics-based nanotechnology with ultra-low damping. In addition, SWs at large wave vector are found to exhibit the non-reciprocal properties relevant for new concepts in nanoscale SW-based logics. We expect our results to provide the basis for coherent data processing with SWs at GHz rates and in large arrays of cellular magnetic arrays, thereby boosting the envisioned image processing and speech recognition.

Figure 1

(a) Sketch of the YIG film with integrated CPWs. The microwave magnetic field h_rf (circles) and the different spin-wave propagation directions are indicated. (b) Excitation spectrum I(k) obtained by Fourier transformation of i_rf (in-plane component). The inset shows the same chart with a logarithmic y-axis scale in order to highlight higher-order modes. (c) Spin wave spectrum of S₁₂ (transmission), meaning spin waves were excited at CPW2 and detected at CPW1. The applied in-plane field amounted to −2 mT (θ = 0, parallel to CPW lines). In the inset we compare spectra S₁₂ (red line) and S₂₁ (black line) taken at −2 mT. (d) Color-coded spectra of spin-wave propagation data S₁₂ as a function of H (θ = 0). The spectrum shown in (c) is extracted from the white dotted line in (d). The coercive (reversal) field is about 0.5 mT.

Figure 2

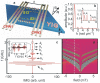
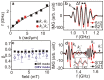
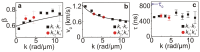
(a) Calculated dispersion relation f(k) (line) compared to experimentally observed eigen-frequencies at 5 mT (symbols). Squares (circles) indicate eigenfrequencies attributed to wave vectors from k₁ to k₇ ( and ). (b) Spin wave spectra of mode k₁ extracted from transmission data S₂₁ (black squares) and S₁₂ (red circles) taken at 5 mT. Amplitudes are different attributed to nonreciprocity. From the frequency separation Δf we calculate the group velocity. (c) Nonreciprocity parameter β as a function of applied field calculated for the mode k₁ from transmission data of S₁₂ and S₂₁. The black squares represent the DE mode (θ = 0), and the open blue dots are for the BV mode (θ = 90 deg). (d) Spin wave spectra of k₂ and k₃ modes extracted from S₂₁ (red circles) and S₁₂ (black squares) transmission data at 5 mT. Modes attributed to the out-of-plane field component of h_rf are marked by a prime. The inset enlarges the signal near .

Figure 3

(a) Nonreciprocity parameter β calculated for different vectors k from transmission data. Black squares show CPW excitation from k₁ to k₇ modes. Red dots show out-of-plane component CPW excitations. The black line is the calculated curve using equations (1) and (2) and f(k) from Fig. 2a. (b) Group velocity of DE spin waves with different vectors k. The line indicates the group velocity calculated from the dispersion relation in Fig. 2a. (c) Spin wave relaxation time calculated from equation (4) using experimental data. The arrow indicates the value τ₀ calculated from the damping parameter α using equation (5). All data are for μ₀H = 5 mT. Black squares show CPW excitation from k₁ to k₇ modes. Red dots show out-of-plane component CPW excitations.

Figure 4

(a) Decay lengths l_d extracted at 5 mT from measured scattering parameters and the data of Fig. 3a according to equation (1). (b) Color-coded plot of spin-wave propagation data of S₂₁ as a function of H (θ = 0). The spin waves are excited at CPW1 and detected at CPW2.

Figure 5. SEM image of the integrated CPWs on the YIG thin film.

The parameter s indicates the propagation distance being 30 μm. The propagation directions of S₁₂ and S₂₁ are indicated. The angle θ of the applied field is defined.

Figure 6. Spectrum S₁₁ taken in reflection configuration using one-and-the-same CPW at 30 mT (θ = 0).

The imaginary part of the signal is shown.

Figure 7. Red vertical arrows indicate in-plane k vectors that are relevant for excitations k₁ to k₆ and have been calculated following Refs. , .

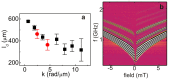
The two tilted blue arrows indicate an appreciable excitation strength at wave vectors and provided by the simulated out-of-plane component of the radiofrequency field h_rf.