Homeostatic structural plasticity can account for topology changes following deafferentation and focal stroke
- PMID: 25360087
- PMCID: PMC4199279
- DOI: 10.3389/fnana.2014.00115
Homeostatic structural plasticity can account for topology changes following deafferentation and focal stroke
Abstract
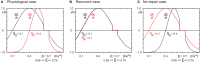
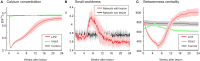
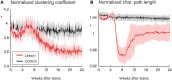
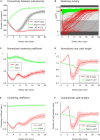
After brain lesions caused by tumors or stroke, or after lasting loss of input (deafferentation), inter- and intra-regional brain networks respond with complex changes in topology. Not only areas directly affected by the lesion but also regions remote from the lesion may alter their connectivity-a phenomenon known as diaschisis. Changes in network topology after brain lesions can lead to cognitive decline and increasing functional disability. However, the principles governing changes in network topology are poorly understood. Here, we investigated whether homeostatic structural plasticity can account for changes in network topology after deafferentation and brain lesions. Homeostatic structural plasticity postulates that neurons aim to maintain a desired level of electrical activity by deleting synapses when neuronal activity is too high and by providing new synaptic contacts when activity is too low. Using our Model of Structural Plasticity, we explored how local changes in connectivity induced by a focal loss of input affected global network topology. In accordance with experimental and clinical data, we found that after partial deafferentation, the network as a whole became more random, although it maintained its small-world topology, while deafferentated neurons increased their betweenness centrality as they rewired and returned to the homeostatic range of activity. Furthermore, deafferentated neurons increased their global but decreased their local efficiency and got longer tailed degree distributions, indicating the emergence of hub neurons. Together, our results suggest that homeostatic structural plasticity may be an important driving force for lesion-induced network reorganization and that the increase in betweenness centrality of deafferentated areas may hold as a biomarker for brain repair.
Keywords: deafferentation; epileptogenesis; focal retinal lesion; homeostatic plasticity; neuronal network model; stroke; structural plasticity; topology.
Figures
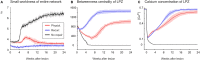
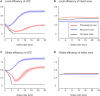
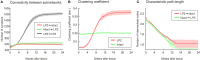
Similar articles
-
Homeostatic structural plasticity increases the efficiency of small-world networks.Front Synaptic Neurosci. 2014 Apr 1;6:7. doi: 10.3389/fnsyn.2014.00007. eCollection 2014. Front Synaptic Neurosci. 2014. PMID: 24744727 Free PMC article.
-
A model for cortical rewiring following deafferentation and focal stroke.Front Comput Neurosci. 2009 Aug 4;3:10. doi: 10.3389/neuro.10.010.2009. eCollection 2009. Front Comput Neurosci. 2009. PMID: 19680468 Free PMC article.
-
Altered topology of large-scale structural brain networks in chronic stroke.Brain Commun. 2019 Oct 4;1(1):fcz020. doi: 10.1093/braincomms/fcz020. eCollection 2019. Brain Commun. 2019. PMID: 32954263 Free PMC article.
-
Synaptic Plasticity Shapes Brain Connectivity: Implications for Network Topology.Int J Mol Sci. 2019 Dec 8;20(24):6193. doi: 10.3390/ijms20246193. Int J Mol Sci. 2019. PMID: 31817968 Free PMC article. Review.
-
Opposing Effects of Neuronal Activity on Structural Plasticity.Front Neuroanat. 2016 Jun 28;10:75. doi: 10.3389/fnana.2016.00075. eCollection 2016. Front Neuroanat. 2016. PMID: 27445713 Free PMC article. Review.
Cited by
-
Microanatomical study of pyramidal neurons in the contralesional somatosensory cortex after experimental ischemic stroke.Cereb Cortex. 2023 Feb 7;33(4):1074-1089. doi: 10.1093/cercor/bhac121. Cereb Cortex. 2023. PMID: 35353195 Free PMC article.
-
Associative properties of structural plasticity based on firing rate homeostasis in recurrent neuronal networks.Sci Rep. 2018 Feb 28;8(1):3754. doi: 10.1038/s41598-018-22077-3. Sci Rep. 2018. PMID: 29491474 Free PMC article.
-
Network Plasticity as Bayesian Inference.PLoS Comput Biol. 2015 Nov 6;11(11):e1004485. doi: 10.1371/journal.pcbi.1004485. eCollection 2015 Nov. PLoS Comput Biol. 2015. PMID: 26545099 Free PMC article.
-
Activation of dominant hemisphere association cortex during naming as a function of cognitive performance in mild traumatic brain injury: Insights into mechanisms of lexical access.Neuroimage Clin. 2017 Jun 23;15:741-752. doi: 10.1016/j.nicl.2017.06.029. eCollection 2017. Neuroimage Clin. 2017. PMID: 28702351 Free PMC article.
-
Neuronal boost to evolutionary dynamics.Interface Focus. 2015 Dec 6;5(6):20150074. doi: 10.1098/rsfs.2015.0074. Interface Focus. 2015. PMID: 26640653 Free PMC article.
References
LinkOut - more resources
Full Text Sources
Other Literature Sources

