Probabilistic cognition in two indigenous Mayan groups

Abstract

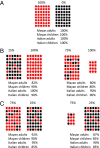
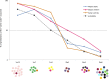
Is there a sense of chance shared by all individuals, regardless of their schooling or culture? To test whether the ability to make correct probabilistic evaluations depends on educational and cultural guidance, we investigated probabilistic cognition in preliterate and prenumerate Kaqchikel and K'iche', two indigenous Mayan groups, living in remote areas of Guatemala. Although the tested individuals had no formal education, they performed correctly in tasks in which they had to consider prior and posterior information, proportions and combinations of possibilities. Their performance was indistinguishable from that of Mayan school children and Western controls. Our results provide evidence for the universal nature of probabilistic cognition.

Keywords: cognitive development; literacy; number cognition; numeracy; probabilistic cognition.

Fig. 1.

Location of the three Guatemalan departments in which the studies were conducted, from left to right: Sololà, Chimaltenango and Sacatepéquez.

Fig. 2.

Performance of Maya and Italian participants in tasks asking for a prior and/or posterior probability evaluation. In the prior task (A), participants had to bet on the color of a randomly drawn chip. In the posterior task (B), participants had to bet on the color of a randomly drawn chip whose shape was indicated by the experimenter. In the updating task (C), participants had to make both a prior and a posterior bet. The grey line indicates the possibilities compatible with the evidence, namely, the shape of the drawn chip: in B, the experimenter has drawn a square chip; in C, she has drawn a round chip. For each task, the figure reports the percentage of participants making the optimal bet.

Fig. 3.

Performance of Maya and Italian controls in tasks in which they had to bet on which of two sets was more likely to yield a red, winning token. The percentage of winning tokens is shown on the top of each set. In A and B, one or both sets contained just winning tokens. In C, both sets contained a proportion of winning tokens. In one task (left panel), the favorable set contained a larger proportion as well as a greater number of winning tokens. In the other task (right panel), it contained a larger proportion but not a greater number of winning tokens. The percentage of participants making the optimal bet is reported on the bottom of each task.

Fig. 4.

Percentage of the “same color” predictions in six tasks in which participants had to bet on whether two randomly chosen tokens would have the same color or two different colors. The optimal bets consisted in predicting “same color” in the first two tasks and “different colors” in the last three tasks. In the third task, the two predictions had the same probability to be correct. The dotted line indicates the probability of the “same color” outcome.