A maximum-likelihood estimation of pairwise relatedness for autopolyploids
- PMID: 25370210
- PMCID: PMC4815632
- DOI: 10.1038/hdy.2014.88
A maximum-likelihood estimation of pairwise relatedness for autopolyploids
Abstract
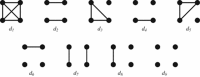
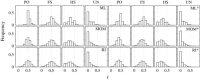
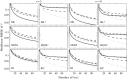
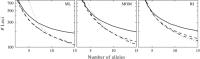
Relatedness between individuals is central to ecological genetics. Multiple methods are available to quantify relatedness from molecular data, including method-of-moment and maximum-likelihood estimators. We describe a maximum-likelihood estimator for autopolyploids, and quantify its statistical performance under a range of biologically relevant conditions. The statistical performances of five additional polyploid estimators of relatedness were also quantified under identical conditions. When comparing truncated estimators, the maximum-likelihood estimator exhibited lower root mean square error under some conditions and was more biased for non-relatives, especially when the number of alleles per loci was low. However, even under these conditions, this bias was reduced to be statistically insignificant with more robust genetic sampling. We also considered ambiguity in polyploid heterozygote genotyping and developed a weighting methodology for candidate genotypes. The statistical performances of three polyploid estimators under both ideal and actual conditions (including inbreeding and double reduction) were compared. The software package POLYRELATEDNESS is available to perform this estimation and supports a maximum ploidy of eight.
Figures
Similar articles
-
Maximum-likelihood estimation of relatedness.Genetics. 2003 Mar;163(3):1153-67. doi: 10.1093/genetics/163.3.1153. Genetics. 2003. PMID: 12663552 Free PMC article.
-
A pairwise relatedness estimator for polyploids.Mol Ecol Resour. 2014 Jul;14(4):734-44. doi: 10.1111/1755-0998.12217. Epub 2014 Jan 27. Mol Ecol Resour. 2014. PMID: 24460904
-
Population genetics of autopolyploids under a mixed mating model and the estimation of selfing rate.Mol Ecol Resour. 2016 Jan;16(1):103-17. doi: 10.1111/1755-0998.12431. Epub 2015 Jun 3. Mol Ecol Resour. 2016. PMID: 25981126
-
Recent progress and challenges in population genetics of polyploid organisms: an overview of current state-of-the-art molecular and statistical tools.Mol Ecol. 2014 Jan;23(1):40-69. doi: 10.1111/mec.12581. Epub 2013 Nov 27. Mol Ecol. 2014. PMID: 24188632 Review.
-
The Analysis of Polyploid Genetic Data.J Hered. 2018 Mar 16;109(3):283-296. doi: 10.1093/jhered/esy006. J Hered. 2018. PMID: 29385510 Review.
Cited by
-
Estimating Relatedness Between Malaria Parasites.Genetics. 2019 Aug;212(4):1337-1351. doi: 10.1534/genetics.119.302120. Epub 2019 Jun 17. Genetics. 2019. PMID: 31209105 Free PMC article.
-
Genotypic Frequencies at Equilibrium for Polysomic Inheritance Under Double-Reduction.G3 (Bethesda). 2019 May 7;9(5):1693-1706. doi: 10.1534/g3.119.400132. G3 (Bethesda). 2019. PMID: 30910817 Free PMC article.
-
A Semi-Automated SNP-Based Approach for Contaminant Identification in Biparental Polyploid Populations of Tropical Forage Grasses.Front Plant Sci. 2021 Oct 22;12:737919. doi: 10.3389/fpls.2021.737919. eCollection 2021. Front Plant Sci. 2021. PMID: 34745171 Free PMC article.
-
Estimation of Molecular Pairwise Relatedness in Autopolyploid Crops.G3 (Bethesda). 2020 Dec 3;10(12):4579-4589. doi: 10.1534/g3.120.401669. G3 (Bethesda). 2020. PMID: 33051262 Free PMC article.
-
Biased social chromosome transmission in males of the fire ant Solenopsis invicta.G3 (Bethesda). 2025 Feb 5;15(2):jkae289. doi: 10.1093/g3journal/jkae289. G3 (Bethesda). 2025. PMID: 39657264 Free PMC article.
References
-
- Charpentier MJE, Fontaine MC, Cherel E, Renoult JP, Jenkins T, Benoit L et al. (2012). Genetic structure in a dynamic baboon hybrid zone corroborates behavioural observations in a hybrid population. Mol Ecol 21: 715–731. - PubMed
-
- Darlington CD. (1929). Chromosome behaviour and structural hybridity in the tradescantiae. J Genet 21: 207–286.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

