Inference of epidemiological dynamics based on simulated phylogenies using birth-death and coalescent models
- PMID: 25375100
- PMCID: PMC4222655
- DOI: 10.1371/journal.pcbi.1003913
Inference of epidemiological dynamics based on simulated phylogenies using birth-death and coalescent models
Abstract
Quantifying epidemiological dynamics is crucial for understanding and forecasting the spread of an epidemic. The coalescent and the birth-death model are used interchangeably to infer epidemiological parameters from the genealogical relationships of the pathogen population under study, which in turn are inferred from the pathogen genetic sequencing data. To compare the performance of these widely applied models, we performed a simulation study. We simulated phylogenetic trees under the constant rate birth-death model and the coalescent model with a deterministic exponentially growing infected population. For each tree, we re-estimated the epidemiological parameters using both a birth-death and a coalescent based method, implemented as an MCMC procedure in BEAST v2.0. In our analyses that estimate the growth rate of an epidemic based on simulated birth-death trees, the point estimates such as the maximum a posteriori/maximum likelihood estimates are not very different. However, the estimates of uncertainty are very different. The birth-death model had a higher coverage than the coalescent model, i.e. contained the true value in the highest posterior density (HPD) interval more often (2-13% vs. 31-75% error). The coverage of the coalescent decreases with decreasing basic reproductive ratio and increasing sampling probability of infecteds. We hypothesize that the biases in the coalescent are due to the assumption of deterministic rather than stochastic population size changes. Both methods performed reasonably well when analyzing trees simulated under the coalescent. The methods can also identify other key epidemiological parameters as long as one of the parameters is fixed to its true value. In summary, when using genetic data to estimate epidemic dynamics, our results suggest that the birth-death method will be less sensitive to population fluctuations of early outbreaks than the coalescent method that assumes a deterministic exponentially growing infected population.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures

 and
and  (
( ). See Figure S1 for the plots of other parameter settings.
). See Figure S1 for the plots of other parameter settings.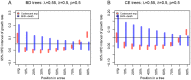
 and
and  (
( ), we modified all 100 birth-death trees (A) and all 100 coalescent trees (B) by branch extension. The unchanged tree is denoted as “orig” on x-axis. We added 48 units of time, roughly corresponding to the full length of the longest trees, to the branches. We extended the branches that were present in the tree at 10% of the tree (going from the root), at 20%, 30%, 40%, 50%, 60%, 70%, 80%, 90% (see x-axis from left to right). We then re-estimated the growth rate parameter for each such tree. Unlike in previous plot, here we display a summary in form of the median values of the start and the end of the 95% HPD intervals, and the median of the medians of the posterior estimates for all 100 trees per setting.
), we modified all 100 birth-death trees (A) and all 100 coalescent trees (B) by branch extension. The unchanged tree is denoted as “orig” on x-axis. We added 48 units of time, roughly corresponding to the full length of the longest trees, to the branches. We extended the branches that were present in the tree at 10% of the tree (going from the root), at 20%, 30%, 40%, 50%, 60%, 70%, 80%, 90% (see x-axis from left to right). We then re-estimated the growth rate parameter for each such tree. Unlike in previous plot, here we display a summary in form of the median values of the start and the end of the 95% HPD intervals, and the median of the medians of the posterior estimates for all 100 trees per setting.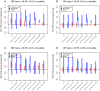
 (
( ), we modified the birth-death tree simulations to include periods of higher (
), we modified the birth-death tree simulations to include periods of higher ( ) and lower sampling (either
) and lower sampling (either  , subfigures A and B, or
, subfigures A and B, or  , subfigures C and D). We simulated 100 birth-death trees (A and C) and corresponding coalescent trees (B and D) under various sampling schemes (see x-axis annotation). We display a summary in form of the median values of the start and the end of the 95% HPD intervals, and the median of the medians of the posterior estimates for all 100 trees per setting. For the settings where the constant rate birth-death method produced very severe biases, we also analysed the trees with the birth-death skyline model with 10 intervals for the sampling probability (BDSKY, light-blue lines). The summary for trees simulated under constant sampling
, subfigures C and D). We simulated 100 birth-death trees (A and C) and corresponding coalescent trees (B and D) under various sampling schemes (see x-axis annotation). We display a summary in form of the median values of the start and the end of the 95% HPD intervals, and the median of the medians of the posterior estimates for all 100 trees per setting. For the settings where the constant rate birth-death method produced very severe biases, we also analysed the trees with the birth-death skyline model with 10 intervals for the sampling probability (BDSKY, light-blue lines). The summary for trees simulated under constant sampling  throughout, is represented on the very left of each figure (
throughout, is represented on the very left of each figure ( on the x-axis). Next, we varied the sampling as to e.g. sample no tips (
on the x-axis). Next, we varied the sampling as to e.g. sample no tips ( ) in the early phases (
) in the early phases ( until
until  ) when going forward in time and then sampling all the tips that die (
) when going forward in time and then sampling all the tips that die ( ) from
) from  onward (corresponding to the setting denoted as “p = 0 from t = 0 to t = 9”).
onward (corresponding to the setting denoted as “p = 0 from t = 0 to t = 9”).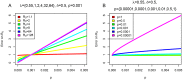
 , i.e. estimated
, i.e. estimated  /true
/true  , and the sampling probability
, and the sampling probability  is plotted. The values
is plotted. The values  and
and  are fixed. For different
are fixed. For different  ,
,  , and
, and  and
and  , we calculate
, we calculate  and
and  , and plot the impact on
, and plot the impact on  error when changing
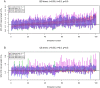
error when changing  during inference using Equation (3) in the Supplementary Material S1. In (B) we display how error on
during inference using Equation (3) in the Supplementary Material S1. In (B) we display how error on  depends on different assumptions of
depends on different assumptions of  during inference for
during inference for  , and
, and  and an array of true sampling probability
and an array of true sampling probability  used for calculating
used for calculating  and
and  .
.
 and
and  (
( ), we estimated the
), we estimated the  parameter from the birth-death trees (A) and the coalescent trees (B) using four methods. First, using the coalescent posterior estimates of the growth rate
parameter from the birth-death trees (A) and the coalescent trees (B) using four methods. First, using the coalescent posterior estimates of the growth rate  and the true
and the true  , we obtained
, we obtained 


 (red bars). Second, we used the birth-death posterior estimates of
(red bars). Second, we used the birth-death posterior estimates of  (trees analysed under uniform priors for
(trees analysed under uniform priors for  ,
,  , and
, and  ), and the true
), and the true  in the post-processing (blue bars), similar to the procedure used for the coalescent. Third, we also analyzed the trees by fixing the prior on the death rate
in the post-processing (blue bars), similar to the procedure used for the coalescent. Third, we also analyzed the trees by fixing the prior on the death rate  to the true value,
to the true value,  (green bars) or by fixing the prior on the sampling probability
(green bars) or by fixing the prior on the sampling probability  to the true value,
to the true value,  (purple bars) during the MCMC analysis. Note that y-axis now displays 95% HPD of the
(purple bars) during the MCMC analysis. Note that y-axis now displays 95% HPD of the  parameter, and within each figure, the trees (simulations) are ordered (x-axis) by the median estimate of growth rate
parameter, and within each figure, the trees (simulations) are ordered (x-axis) by the median estimate of growth rate  parameter estimated by the coalescent on the birth-death trees.
parameter estimated by the coalescent on the birth-death trees.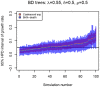
 (blue bars) and the coalescent model with a deterministic exponentially growing population (red bars). Here we used
(blue bars) and the coalescent model with a deterministic exponentially growing population (red bars). Here we used  and sampling probability
and sampling probability  (
( ). See Figure S15 for the plots of other parameter settings.
). See Figure S15 for the plots of other parameter settings.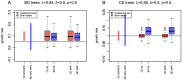
 and
and  (
( ), we display the ML and MAP estimates for the birth-death trees (A) and the coalescent trees (B). As a comparison, the median values of the start and the end of the 95% HPD intervals, and the median of the medians of the posterior estimates for all 100 trees per setting are also displayed. The true value of the growth rate parameter, i.e. the value under which the trees were simulated, is displayed as a black horizontal bar. See Figures S17 and S18 for the plots of other parameter settings.
), we display the ML and MAP estimates for the birth-death trees (A) and the coalescent trees (B). As a comparison, the median values of the start and the end of the 95% HPD intervals, and the median of the medians of the posterior estimates for all 100 trees per setting are also displayed. The true value of the growth rate parameter, i.e. the value under which the trees were simulated, is displayed as a black horizontal bar. See Figures S17 and S18 for the plots of other parameter settings.References
-
- Anderson R, May R (1991) Infectious diseases of humans. Dynamics and Control Oxford University Press, Oxford, New York, Tokyo.
-
- Dietz K (1975) Transmission and control of arbovirus diseases. Epidemiology 104–121.
-
- Kermack W, McKendrick A (1927) A contribution to the mathematical theory of epidemics. Proceedings of the Royal Society of London Series A 115: 700–721.
-
- Felsenstein J (2004) Inferring phylogenies, volume 2. Sinauer Associates Sunderland
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

