Phase separation and emergent structures in an active nematic fluid

Abstract

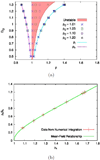
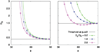
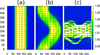
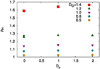
We consider a phenomenological continuum theory for an active nematic fluid and show that there exists a universal, model-independent instability which renders the homogeneous nematic state unstable to order fluctuations. Using numerical and analytic tools we show that, in the vicinity of a critical point, this instability leads to a phase-separated state in which the ordered regions form bands in which the direction of nematic order is perpendicular to the direction of the density gradient. We argue that the underlying mechanism that leads to this phase separation is a universal feature of active fluids of different symmetries.

FIG. 1

(color online) Phase behavior of the system as a function of the mean density of the system (ρ₀) and the activity (D_Q). Below the critical density for the order disorder transition (i.e., ρ < 1) the homogeneous disordered state is stable. For any density ρ ≥ 1, there is an activity D_Q above which the homogeneous ordered state is unstable. This region, in which there is no stable homogeneous state, is shown in red.

FIG. 2

(color online) (a) A plot of the density and order of a typical system (ρ₀ = 1.01, D_Q = 0.8) that has phase-separated into bands. The lines show the magnitude (by the length) and direction of nematic ordering. The light region is a band of high density with nematic ordering along the band. The axes show the position in the system in dimensionless ‘diffusion lengths’ and the scale bar shows the density. (b) Profiles of the density (top) and order (ρS, on bottom), taken perpendicular to the direction of ordering in the bands.

FIG. 3

(color online) (a) For fixed activity, several initial densities in the unstable region are chosen. The final densities in the banded state (ρ_h and ρ_l) are found to be independent of the initial density, as the points for different initial densities fall on the same curve. (b) The measured value of order (ρS) as a function of ρ_h. The solid line is the mean field prediction $\rho h\sqrt{\frac{2({\rho }_h-1)}{{\rho }_h+1}}$. Excellent agreement is found substantiating the picture that the bands are just phase coexistence between a high density nematic and a low density isotropic state.

FIG. 4

(color online) Plot of D_Q(ϕ), the value of activity at which spatial fluctuations in the direction ϕ become unstable. Left panel : ρ = 1.01, close to the critical point, when D_Q is monotonic and is smallest in the ϕ = 90° direction. Right panel : ρ = 2.0, D_Q becomes non monotonic when the Frank elastic constant becomes small compared to the kinetic terms. The horizontal line at D_Q(90°) is a guide to the eye.

FIG. 5

(color online) Identifying the directions in space associated with destabilizing fluctuations for different choices of parameters of the continuum theory. When D_ρ/D_E becomes large, the instability persists to large values of density and is spread over a wider range of ϕ

FIG. 6

(color online) The density of the ordered phase (ρ_h) is shown for a range of D_ρ, D_E, and D_Q respectively. ρ_h is insensitive to D_ρ and D_E, especially for small D_Q.

FIG. 7

(color online) The plots above show the progression of the structures which form as D_ρ/D_E is increased. The density is represented as a heat map, and the magnitude and direction of order is represented by the length and orientation of the lines (as in Fig. 2) after 90,000 diffusion times. These systems all have parameters ρ₀ = 1.10, D_Q = 1.30 and D_E = 1.20. (a) For D_ρ = 0.80D_E, the band of the ordered phase is stable. (b) For D_ρ = 1.20D_E the band is unstable to a large wave-length instability which causes it to bend and eventually break. (c) For D_ρ = 2.50D_E the band breaks down quickly and a structure with fluctuations on a much smaller length scale forms. This structure is dynamical, and the order at the edges fluctuates, but it persists for over a hundred thousand of diffusion times.

FIG. 8

(color online) The density of the ordered phase (ρ_H) is shown for a few different values of the coefficient of the kinetic term (D_ρ) in the case where that kinetic term is proportional to S. When compared to the plot on the left in Fig. 6 it can be seen that the change to the kinetic term has not significantly altered the density of the ordered phase.