The interplay of plasticity and adaptation in neural circuits: a generative model

Abstract

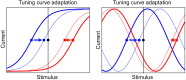
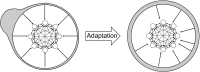
Multiple neural and synaptic phenomena take place in the brain. They operate over a broad range of timescales, and the consequences of their interplay are still unclear. In this work, I study a computational model of a recurrent neural network in which two dynamic processes take place: sensory adaptation and synaptic plasticity. Both phenomena are ubiquitous in the brain, but their dynamic interplay has not been investigated. I show that when both processes are included, the neural circuit is able to perform a specific computation: it becomes a generative model for certain distributions of input stimuli. The neural circuit is able to generate spontaneous patterns of activity that reproduce exactly the probability distribution of experienced stimuli. In particular, the landscape of the phase space includes a large number of stable states (attractors) that sample precisely this prior distribution. This work demonstrates that the interplay between distinct dynamical processes gives rise to useful computation, and proposes a framework in which neural circuit models for Bayesian inference may be developed in the future.

Keywords: Bayesian inference; attractor model; dynamical systems; generative model; sensory adaptation; synaptic plasticity.

Figure 1

Schematic illustration of the neural circuit model with its tuning curves and recurrent connections. Each circle represents one neuron and each arrow a synaptic connection. Each rectangle shows a tuning curve for one neuron, namely the external current afferent to that neuron plotted as a function of the stimulus value. Left: sigmoidal tuning curves. Right: periodic tuning curves.

Figure 2

The adaptation mechanism, by which tuning curves of neurons are modified according to the presented stimulus. Tuning curves of two neurons are shown, one neuron in blue and the other one in red, before and after adaptation (full and dashed line, respectively). The presented stimulus is indicated by the black dot and the vertical black line. The tuning offsets of the two neurons are shown by the blue and red dots. Tuning offsets are attracted by the stimulus, as shown by the arrows. Left: sigmoidal tuning curves. Right: periodic tuning curves.

Figure 3

Distribution of stimuli p(α) (probability density, black curve) from which the sequence of input stimuli is drawn, and the stable fixed points of the spontaneous dynamics (attractors, blue stars), referred to as “retrieved patterns.” Four example simulations are shown in the four panels. Each stable fixed point is denoted by a star along the stimulus space. Different rows in each panel correspond to the 10 sessions of that simulation, ordered from top to bottom. In early sessions, a few attractors tend to locate near the modes of the probability density. In late sessions, several attractors sample the entire space of stimuli in proportion to the their likelihood. A histogram of the attractors from 1000 sessions (blue bars) is supermposed to the probability density of stimuli.

Figure 4

Effect of adaptation on the representation of stimuli. Left: illustration of the neural circuit model, same as in Figure 1. The tuning curves of different neurons are not shown here, but are still represented by the arrows pointing from the external circle to the neural circuit. The gray shading illustrates the distribution of external stimuli according to the network selectivity: the bump on the top left of the figure implies that most stimuli are presented in that region. By definition, a stimulus presented at a given place of the neural circuit is intended as equal to the tuning offset of the corresponding neuron. Right: after adaptation, the tuning curves of neurons are changed, as shown by the displacement of the arrows from the bulk of the stimulus distribution. As a consequence, the stimulus distribution in gray shading now appears uniform across the network (uniform gray shading around the circle).

Figure 5

Number of attractor states as a function of session number, timescale τ (left), and number of neurons (right). The number of attractor states increases in subsequent sessions and for slower timescales. The scaling of the number of attractors with respect to the number of neurons is ~N^2/3.