The quartic piecewise-linear criterion for the multiaxial yield behavior of human trabecular bone

Abstract

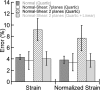
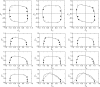
Prior multiaxial strength studies on trabecular bone have either not addressed large variations in bone volume fraction and microarchitecture, or have not addressed the full range of multiaxial stress states. Addressing these limitations, we utilized micro-computed tomography (lCT) based nonlinear finite element analysis to investigate the complete 3D multiaxial failure behavior of ten specimens (5mm cube) of human trabecular bone, taken from three anatomic sites and spanning a wide range of bone volume fraction (0.09–0.36),mechanical anisotropy (range of E3/E1¼3.0–12.0), and microarchitecture. We found that most of the observed variation in multiaxial strength behavior could be accounted for by normalizing the multiaxial strength by specimen-specific values of uniaxial strength (tension,compression in the longitudinal and transverse directions). Scatter between specimens was reduced further when the normalized multiaxial strength was described in strain space.The resulting multiaxial failure envelope in this normalized-strain space had a rectangular boxlike shape for normal–normal loading and either a rhomboidal box like shape or a triangular shape for normal-shear loading, depending on the loading direction. The finite element data were well described by a single quartic yield criterion in the 6D normalized strain space combined with a piecewise linear yield criterion in two planes for normalshear loading (mean error SD: 4.660.8% for the finite element data versus the criterion).This multiaxial yield criterion in normalized-strain space can be used to describe the complete 3D multiaxial failure behavior of human trabecular bone across a wide range of bone volume fraction, mechanical anisotropy, and microarchitecture.

Fig. 1

Yield strain (top row), normalized-yield-strain (middle row), and normalized-yield-stress (bottom row) in the three normal biaxial planes, showing individual responses for all ten specimens. The same tissue-level material properties were assumed for all specimens. For each biaxial plane, the virtually applied normal strain (top and middle row) and normal stress (bottom row) in the third normal direction is zero. Scatter was much less when the normalized-yield-strain was used to describe the multiaxial failure behavior.

Fig. 2

Normalized-yield-strain in the nine normal-shear biaxial planes, showing individual responses for all ten specimens. For each biaxial plane, the virtually applied normal and shear strains in the other two normal and shear directions, respectively, are zero.

Fig. 3

Mean absolute error (±SD, n = 10 specimens) of the specimen-specific mathematical fit versus the finite element computed normalized-yield-strain data for (a) the normal (only) 3D space using the quartic yield criterion, (b) the seven normal-shear planes (${\stackrel{\wedge }{\varepsilon }}_{11}-{\stackrel{\wedge }{\gamma }}_{12}$, ${\stackrel{\wedge }{\varepsilon }}_{11}-{\stackrel{\wedge }{\gamma }}_{13}$, ${\stackrel{\wedge }{\varepsilon }}_{11}-{\stackrel{\wedge }{\gamma }}_{23}$, ${\stackrel{\wedge }{\varepsilon }}_{22}-{\stackrel{\wedge }{\gamma }}_{12}$, ${\stackrel{\wedge }{\varepsilon }}_{22}-{\stackrel{\wedge }{\gamma }}_{13}$, ${\stackrel{\wedge }{\varepsilon }}_{22}-{\stackrel{\wedge }{\gamma }}_{23}$, ${\stackrel{\wedge }{\varepsilon }}_{33}-{\stackrel{\wedge }{\gamma }}_{12}$) using the quartic yield criterion, (c) the two normal-shear planes (${\stackrel{\wedge }{\varepsilon }}_{33}-{\stackrel{\wedge }{\gamma }}_{13}$, ${\stackrel{\wedge }{\varepsilon }}_{33}-{\stackrel{\wedge }{\gamma }}_{23}$) using the quartic yield criterion, and (d) the two normal-shear planes (${\stackrel{\wedge }{\varepsilon }}_{33}-{\stackrel{\wedge }{\gamma }}_{13}$, ${\stackrel{\wedge }{\varepsilon }}_{33}-{\stackrel{\wedge }{\gamma }}_{23}$) planes using a combination of the quartic and piecewise linear yield criteria.

Fig. 4

Yield envelopes in the three biaxial normal normalized-strain planes and the nine normal-shear normalized-strain planes for one specimen from the vertebral body (BV/TV = 0.11) using the quartic yield criterion (solid line, Eq. (4)) and the piecewise linear-yield criterion (dashed line, Eq. (5)). For all plots, the solid circles fail in the mode denoted by the horizontal axis and the hollow circles fail in the mode denoted by the vertical axis. For the quartic criterion alone, the mean error of the fit was 4.2% for the combined ${\stackrel{\wedge }{\varepsilon }}_{33}-{\stackrel{\wedge }{\varepsilon }}_{11}$, ${\stackrel{\wedge }{\varepsilon }}_{33}-{\stackrel{\wedge }{\varepsilon }}_{22}$, and ${\stackrel{\wedge }{\varepsilon }}_{22}-{\stackrel{\wedge }{\varepsilon }}_{11}$ planes, 3.1% for the combined ${\stackrel{\wedge }{\varepsilon }}_{11}-{\stackrel{\wedge }{\gamma }}_{12}$, ${\stackrel{\wedge }{\varepsilon }}_{11}-{\stackrel{\wedge }{\gamma }}_{13}$, ${\stackrel{\wedge }{\varepsilon }}_{11}-{\stackrel{\wedge }{\gamma }}_{23}$, ${\stackrel{\wedge }{\varepsilon }}_{22}-{\stackrel{\wedge }{\gamma }}_{12}$, ${\stackrel{\wedge }{\varepsilon }}_{22}-{\stackrel{\wedge }{\gamma }}_{13}$, ${\stackrel{\wedge }{\varepsilon }}_{22}-{\stackrel{\wedge }{\gamma }}_{23}$, and ${\stackrel{\wedge }{\varepsilon }}_{33}-{\stackrel{\wedge }{\gamma }}_{12}$ planes, and 7.5% for the combined ${\stackrel{\wedge }{\varepsilon }}_{33}-{\stackrel{\wedge }{\gamma }}_{13}$ and ${\stackrel{\wedge }{\varepsilon }}_{33}-{\stackrel{\wedge }{\gamma }}_{23}$ planes. For the latter two planes, when the quartic criterion was combined with the piecewise linear criterion (QPL criterion), the mean error reduced to 2.9%. In this case, the assumed failure envelope is the inner surface of the two individual criteria.