Static network structure can stabilize human cooperation
- PMID: 25404308
- PMCID: PMC4260616
- DOI: 10.1073/pnas.1400406111
Static network structure can stabilize human cooperation
Abstract
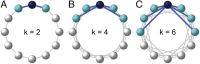
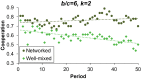
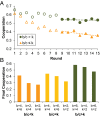
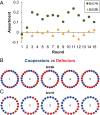
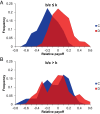
The evolution of cooperation in network-structured populations has been a major focus of theoretical work in recent years. When players are embedded in fixed networks, cooperators are more likely to interact with, and benefit from, other cooperators. In theory, this clustering can foster cooperation on fixed networks under certain circumstances. Laboratory experiments with humans, however, have thus far found no evidence that fixed network structure actually promotes cooperation. Here, we provide such evidence and help to explain why others failed to find it. First, we show that static networks can lead to a stable high level of cooperation, outperforming well-mixed populations. We then systematically vary the benefit that cooperating provides to one's neighbors relative to the cost required to cooperate (b/c), as well as the average number of neighbors in the network (k). When b/c > k, we observe high and stable levels of cooperation. Conversely, when b/c ≤ k or players are randomly shuffled, cooperation decays. Our results are consistent with a quantitative evolutionary game theoretic prediction for when cooperation should succeed on networks and, for the first time to our knowledge, provide an experimental demonstration of the power of static network structure for stabilizing human cooperation.
Keywords: Prisoner’s Dilemma; assortment; economic games; evolutionary game theory; structured populations.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
Similar articles
-
Autonomy promotes the evolution of cooperation in prisoner's dilemma.Phys Rev E. 2020 Oct;102(4-1):042402. doi: 10.1103/PhysRevE.102.042402. Phys Rev E. 2020. PMID: 33212636
-
A condition for cooperation in a game on complex networks.J Theor Biol. 2011 Jan 21;269(1):224-33. doi: 10.1016/j.jtbi.2010.10.033. Epub 2010 Oct 31. J Theor Biol. 2011. PMID: 21044635
-
Green-beard effect predicts the evolution of traitorousness in the two-tag Prisoner's dilemma.J Theor Biol. 2011 Nov 7;288:84-91. doi: 10.1016/j.jtbi.2011.07.023. Epub 2011 Aug 2. J Theor Biol. 2011. PMID: 21821051
-
Review: Game theory of public goods in one-shot social dilemmas without assortment.J Theor Biol. 2012 Apr 21;299:9-20. doi: 10.1016/j.jtbi.2011.06.018. Epub 2011 Jun 24. J Theor Biol. 2012. PMID: 21723299 Review.
-
Cooperation in a generalized age-structured spatial game.J Theor Biol. 2020 Jan 7;484:109995. doi: 10.1016/j.jtbi.2019.109995. Epub 2019 Sep 3. J Theor Biol. 2020. PMID: 31491496 Review.
Cited by
-
Adherence to public institutions that foster cooperation.Nat Commun. 2021 Jun 11;12(1):3567. doi: 10.1038/s41467-021-23783-9. Nat Commun. 2021. PMID: 34117236 Free PMC article.
-
The effects of reputational and social knowledge on cooperation.Proc Natl Acad Sci U S A. 2015 Mar 24;112(12):3647-52. doi: 10.1073/pnas.1415883112. Epub 2015 Mar 9. Proc Natl Acad Sci U S A. 2015. PMID: 25775544 Free PMC article.
-
Human social preferences cluster and spread in the field.Proc Natl Acad Sci U S A. 2020 Sep 15;117(37):22787-22792. doi: 10.1073/pnas.2000824117. Epub 2020 Sep 1. Proc Natl Acad Sci U S A. 2020. PMID: 32873647 Free PMC article.
-
Human cooperation in changing groups in a large-scale public goods game.Nat Commun. 2022 Oct 27;13(1):6399. doi: 10.1038/s41467-022-34160-5. Nat Commun. 2022. PMID: 36302777 Free PMC article.
-
Reinforcement learning account of network reciprocity.PLoS One. 2017 Dec 8;12(12):e0189220. doi: 10.1371/journal.pone.0189220. eCollection 2017. PLoS One. 2017. PMID: 29220413 Free PMC article.
References
-
- Strogatz SH. Exploring complex networks. Nature. 2001;410(6825):268–276. - PubMed
-
- Palla G, Barabási A-L, Vicsek T. Quantifying social group evolution. Nature. 2007;446(7136):664–667. - PubMed
-
- Henrich J, et al. Markets, religion, community size, and the evolution of fairness and punishment. Science. 2010;327(5972):1480–1484. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

