A probabilistic approach to quantify the impact of uncertainty propagation in musculoskeletal simulations

Abstract

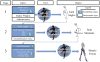
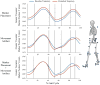
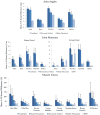
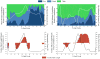
Uncertainty that arises from measurement error and parameter estimation can significantly affect the interpretation of musculoskeletal simulations; however, these effects are rarely addressed. The objective of this study was to develop an open-source probabilistic musculoskeletal modeling framework to assess how measurement error and parameter uncertainty propagate through a gait simulation. A baseline gait simulation was performed for a male subject using OpenSim for three stages: inverse kinematics, inverse dynamics, and muscle force prediction. A series of Monte Carlo simulations were performed that considered intrarater variability in marker placement, movement artifacts in each phase of gait, variability in body segment parameters, and variability in muscle parameters calculated from cadaveric investigations. Propagation of uncertainty was performed by also using the output distributions from one stage as input distributions to subsequent stages. Confidence bounds (5-95%) and sensitivity of outputs to model input parameters were calculated throughout the gait cycle. The combined impact of uncertainty resulted in mean bounds that ranged from 2.7° to 6.4° in joint kinematics, 2.7 to 8.1 N m in joint moments, and 35.8 to 130.8 N in muscle forces. The impact of movement artifact was 1.8 times larger than any other propagated source. Sensitivity to specific body segment parameters and muscle parameters were linked to where in the gait cycle they were calculated. We anticipate that through the increased use of probabilistic tools, researchers will better understand the strengths and limitations of their musculoskeletal simulations and more effectively use simulations to evaluate hypotheses and inform clinical decisions.

Figure 1

A gait trial was analyzed using OpenSim across three stages: inverse kinematics, inverse dynamics, and muscle force optimization. Distributions of sources of uncertainty were inputs to each tool in a probabilistic simulation. To assess the propagation of uncertainty, output distributions from each tool were input into the next tool in the workflow. Output of each tool was used to calculate 5–95 confidence bounds and the sensitivity of the output to each source of uncertainty.

Figure 2

Representative marker trajectory that illustrates simulation of marker placement uncertainty, movement artifact uncertainty, and the combination of the two sources. Marker placement uncertainty was modeled as a constant offset throughout the gait cycle. Movement artifact was modeled using a trajectory that varied within each phase of the gait cycle (each phase separated by vertical lines). The marker set used for segment tracking is shown on the right.

Figure 3

5–95 confidence bounds for each simulation stage output following inverse kinematics (Stage 1), inverse dynamics (Stage 2) and static optimization (Stage 3). Values for the calculated mean 5–95 confidence bounds are displayed. Kinematic and kinetic degrees of freedom were divided into stance and swing periods. The baseline simulation output is represented by the black line.

Figure 4

Mean 5–95 confidence bounds for each individual source of uncertainty for kinematics, joint moments and muscle forces. 5–95 confidence bounds calculated for joint moments were divided into stance and swing periods.

Figure 5

Upper: Relative sensitivity of flexion/extension and adduction/abduction hip moments to foot, shank, and thigh body segment parameters for each time point during the gait cycle. Relative sensitivity is presented as the segment correlation coefficient divided by the sum of the foot, shank, and thigh coefficient. Segment mass to hip flexion moment (Left), medial lateral position of the center of mass and hip adduction moment (Right). Lower: Sensitivity of predicted muscle force to tendon slack length calculated at each time point throughout the gait cycle for medial gastrocnemius (Left) and rectus femoris (right). Uncertainty in tendon slack length influences the point on the force–length curve that these two biarticular muscles operate on throughout the gait cycle. Note: no sensitivity reported when the muscle force is 0.