Biomechanics and mechanobiology of trabecular bone: a review

Abstract

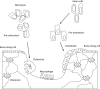
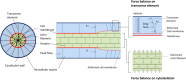
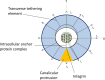
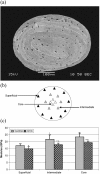
Trabecular bone is a highly porous, heterogeneous, and anisotropic material which can be found at the epiphyses of long bones and in the vertebral bodies. Studying the mechanical properties of trabecular bone is important, since trabecular bone is the main load bearing bone in vertebral bodies and also transfers the load from joints to the compact bone of the cortex of long bones. This review article highlights the high dependency of the mechanical properties of trabecular bone on species, age, anatomic site, loading direction, and size of the sample under consideration. In recent years, high resolution micro finite element methods have been extensively used to specifically address the mechanical properties of the trabecular bone and provide unique tools to interpret and model the mechanical testing experiments. The aims of the current work are to first review the mechanobiology of trabecular bone and then present classical and new approaches for modeling and analyzing the trabecular bone microstructure and macrostructure and corresponding mechanical properties such as elastic properties and strength.

Fig. 1

An illustration of the hierarchical nature of trabecular bone

Fig. 2

An illustration of bone cell population

Fig. 3

Strain-amplification model illustrating the osteocyte process in cross section and longitudinal section. Actin filaments span the process, which is attached to the canalicular wall via transverse elements. Applied loading results in interstitial fluid flow through the pericellular matrix, producing a drag force on the tethering fibers.

Fig. 4

Illustration of an integrin-based strain-amplification model

Fig. 5

(a) Scanning electronmicroscopy image of atrabeculum. (b) Indent locations across the width of a trabeculum. (c) Tissue Young modulus of trabecular bone using nano-indentation from skeletally mature sheep after undergoing overiectomy (OVX). (From Reference with permission.)

Fig. 6

(a) The layout of the cored specimens (S1–S7) demonstrated on a proximal femur image. Three-dimensional visualization of the average (b) modulus (E) with the upper and lower limits of data at each site; and (c) bone volume fraction (BV/TV) distribution of human proximal femur. In (a), sites S1, S4, S6, and S7 form a loop or belt from the femoral head, through the neck and onto the trochanteric region, where the applied load (in a relatively uniform magnitude) traverses through the proximal femur and disburses into the cortical shaft. It is possible that the loads resultant from normal daily activities are mostly translated though this loop, whereas sites S2 and S3 encounter the higher loads applied to the proximal femur for higher impact activities. (From Reference with permission.)

Fig. 7

Schematic flowchart of computing multiscale material properties: (a) representative elementary volume (RVE) homogenization for estimation of the effective material properties of the bone model at all intermediate levels; (b) a correlation between the porosity of the geometrical models and their respective effective material properties; (c) inverse local material properties model as a function of porosity; and (d) computational model verification. (From Reference with permission.)

Fig. 8

Spatial decomposition of trabecular bone. The initial binary image that served as input for our algorithm is shown in panel (a). A skeletonization and optimization algorithm is applied to get a homotopic shape preserving skeleton as shown in panel (b). This skeleton is then point-classified, thus arc-, surface-, border-, and intersection-points are shown in different colors. (c) This point-classified skeleton is then spatially decomposed by removing the intersection points. (d) A two-way multicolor dilation algorithm was applied to find the volumetric extend of each element, yielding in the final spatially decomposed structure. (From Reference with permission.)

Fig. 9

Failure occurs at subregions with the lowest BV/TV values. Subregions number 1, 2, 3, and 4 with the lowest BV/TV values here coincide with the four regions that fail based on the visual data provided by the time-lapsed mechanical testing. (From Reference with permission.)

Fig. 10

Reductions in secant modulus and accumulation of strain with increasing number of load cycles characterized the cyclic behavior of trabecular bone. Failure was defined as the cycle before which a specimen could no longer sustain the prescribed normalized stress, as indicated by a rapid increase in strain upon the subsequent loading cycle. Creep strain was defined by translation along the X-axis (c_k), and damage strain was defined by the difference of the hysteresis loop strains (d_k + d₁). Total strain was the sum (c_k + d_k). (From Reference with permission.)