Piecewise linear and Boolean models of chemical reaction networks

Abstract

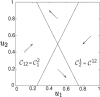
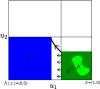
Models of biochemical networks are frequently complex and high-dimensional. Reduction methods that preserve important dynamical properties are therefore essential for their study. Interactions in biochemical networks are frequently modeled using Hill functions ([Formula: see text]). Reduced ODEs and Boolean approximations of such model networks have been studied extensively when the exponent [Formula: see text] is large. However, while the case of small constant [Formula: see text] appears in practice, it is not well understood. We provide a mathematical analysis of this limit and show that a reduction to a set of piecewise linear ODEs and Boolean networks can be mathematically justified. The piecewise linear systems have closed-form solutions that closely track those of the fully nonlinear model. The simpler, Boolean network can be used to study the qualitative behavior of the original system. We justify the reduction using geometric singular perturbation theory and compact convergence, and illustrate the results in network models of a toggle switch and an oscillator.

Figure 1

(a) Nodes u₁, u₂ inhibiting each other’s activity resulting in a switch. The node which starts out stronger suppresses the activity of the other. (b) Nodes u₁, u₂, and u₃ suppress each other in a cyclic fashion. Under certain conditions, this can lead to oscillations.

Figure 2

Subdomains ${\mathcal{R}}_S^T$ for the unit square [0, 1]² (panel a), and chambers of [0, 1]² defined by the asymptotic behavior of the nullclines of Eq. (2) (panel b).

Figure 3

Comparison of the numerical solution of Eq. (2) (dashed black) with the solution of the approximate system as listed in Table 1 (red) for two different values of J (panels (a) and (b)) and the 0-th order approximation (blue). We used J = 5 × 10⁻³ in (a), J = 10⁻³ in (b), and J = 10⁻⁴ in (c). We also used δ = 2 J. (a,b) The solution of the linear approximation started in the subdomain $\mathcal{R}$ (Initial value: u₁ = 0.5, u₂ = 0.25), and as soon as u₂ decreased below δ, we assumed that the solution entered subdomain ${\mathcal{R}}_2$. The approximate solution is discontinuous since when u₂ = δ, the solution jumped (see inset) to the manifold, described by the algebraic part of the linear differential algebraic system prevalent in the subdomain ${\mathcal{R}}_2$, Eq. (7b). The solution finally stopped in the subdomain ${\mathcal{R}}_2^1$. As J gets smaller, the discontinuity becomes negligible and the approximate system from Table 1 converges to the (continuous) 0-th order approximation. (c) The 0-th order approximation (black solid curve) becomes an accurate approximation of the original system as J → 0 (the solution from Table 1 is not shown in panel (c)).

Figure 4

Behavior of nullclines as J decreases. Top: Nullclines of Eq. (2) for J = 10⁻² (left) and J = 10⁻⁴ (right). Bottom: Nullcline $\frac{{\mathit{du}}_2}{\mathit{dt}}=0$ of Eq. (2) (black curve) and the manifold defined by Eq. (7b) (red) for J = 10⁻² and δ = 10⁻2 (left), and J = 10⁻⁴ and δ = 10⁻2 (right).

Figure 5

Left: Solutions of Eq. (2) for J = 10⁻⁴. When a solution is close to the boundary regions of ${\mathcal{C}}_1^2$ and ${\mathcal{C}}_2^1$, they enter the invariant region as shown in Fig. 3b. Right: Graphical representation of the Boolean transitions (00 → 11, 11 → 00, 01 → 01, 10 → 10).

Figure 6

Comparison of the numerical solution of Eq. (10) (dashed black) and the 0-th order approximation (solid black curves) for two different values of J. For (a)–(b) J = 10⁻³; for (c)–(d) J = 10⁻⁴. Panel (e) shows the time series for the 0-th order approximation. Panel (f) shows the time series for the solutions of Eq. (10) using J = 10⁻⁴.

Figure 7

chambers for $W=\left[\begin{array}{ll}1& -1\\ 0& -1\end{array}\right]$ and $b=\left[\begin{array}{r}-0.5\\ 0.6\end{array}\right]$ (left); $W=\left[\begin{array}{rr}2& -1\\ 2& 1\end{array}\right]$ and $b=\left[\begin{array}{l}-0.5\\ -1.5\end{array}\right]$

Figure 8

Chambers and signs of vector field for the linear system given by $W=\left[\begin{array}{rr}-2& -1\\ -2& 1\end{array}\right]$ and $b=\left[\begin{array}{l}1.5\\ 0.5\end{array}\right]$.

Figure 9

Plots of right hand side of Eq. (22) for three different values of J, as functions of x. Other parameters: A = 1, I = .5. This figure suggests that differential equations of the form Eq. (22) can be approximated by linear ODEs in the interior of the domain.

Figure 10

Solutions of Eq. (22) for three different values of J (left: J = 0.1, center: J = 0.01, right: J = 0.001). Other parameters: A = 1, I = .5.

Figure 11

Sets L (blue), L₁ (red), and K (green) in the proof of Theorem 6 for N = 2.

Figure 12

Sets K (light green), K⁰ (dark green and light green), and K¹ (blue) in the proof of Theorem 8 for N = 2.

Figure 13

Plots of right hand side of Eq. (26) for three different values of J, as functions of x, and three different values of n (left: n = 2, center n = 5, right: n = 10). Other parameters: A = 1, I = .5.