Rapid phylogenetic analysis of large samples of recombinant bacterial whole genome sequences using Gubbins
- PMID: 25414349
- PMCID: PMC4330336
- DOI: 10.1093/nar/gku1196
Rapid phylogenetic analysis of large samples of recombinant bacterial whole genome sequences using Gubbins
Abstract
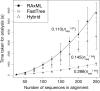
The emergence of new sequencing technologies has facilitated the use of bacterial whole genome alignments for evolutionary studies and outbreak analyses. These datasets, of increasing size, often include examples of multiple different mechanisms of horizontal sequence transfer resulting in substantial alterations to prokaryotic chromosomes. The impact of these processes demands rapid and flexible approaches able to account for recombination when reconstructing isolates' recent diversification. Gubbins is an iterative algorithm that uses spatial scanning statistics to identify loci containing elevated densities of base substitutions suggestive of horizontal sequence transfer while concurrently constructing a maximum likelihood phylogeny based on the putative point mutations outside these regions of high sequence diversity. Simulations demonstrate the algorithm generates highly accurate reconstructions under realistically parameterized models of bacterial evolution, and achieves convergence in only a few hours on alignments of hundreds of bacterial genome sequences. Gubbins is appropriate for reconstructing the recent evolutionary history of a variety of haploid genotype alignments, as it makes no assumptions about the underlying mechanism of recombination. The software is freely available for download at github.com/sanger-pathogens/Gubbins, implemented in Python and C and supported on Linux and Mac OS X.
© The Author(s) 2014. Published by Oxford University Press on behalf of Nucleic Acids Research.
Figures



References
-
- Achtman M. Evolution, population structure, and phylogeography of genetically monomorphic bacterial pathogens. Annu. Rev. Microbiol. 2008;62:53–70. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Molecular Biology Databases

