Simulation study for evaluating the performance of response-adaptive randomization

Abstract

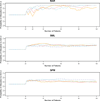
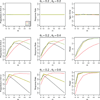
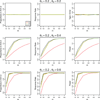
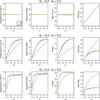
A response-adaptive randomization (RAR) design refers to the method in which the probability of treatment assignment changes according to how well the treatments are performing in the trial. Holding the promise of treating more patients with the better treatments, RARs have been successfully implemented in clinical trials. We compared equal randomization (ER) with three RARs: Bayesian adaptive randomization, sequential maximum likelihood, and sequential posterior mean. We fixed the total number of patients, considered as patient horizon, but varied the number of patients in the trial. Among the designs, we compared the proportion of patients assigned to the superior arm, overall response rate, statistical power, and total patients enrolled in the trial with and without adding an efficacy early stopping rule. Without early stopping, ER is preferred when the number of patients beyond the trial is much larger than the number of patients in the trial. RAR is favored for large treatment difference or when the number of patients beyond the trial is small. With early stopping, the difference between these two types of designs was reduced. By carefully choosing the design parameters, both RAR and ER methods can achieve the desirable statistical properties. Within three RAR methods, we recommend SPM considering the larger proportion in the better arm and higher overall response rate than BAR and similar power and trial size with ER. The ultimate choice of RAR or ER methods depends on the investigator's preference, the trade-off between group ethics and individual ethics, and logistic considerations in the trial conduct, etc.

Keywords: Allocation probability; Bayesian adaptive design; Efficacy early stopping; Operating characteristics; Patient horizon.

Figure 1

Change in the allocation probability during the trial for BAR (top panel), SML (middle panel), and SPM (bottom panel) methods, respectively. We considered five realizations of the trial. The x-axis represents the total number of patients; the y-axis represents the probability of allocation to arm 2, the superior treatment. The true response rates are θ₁ = 0.4 and θ₂ = 0.7.

Figure 2

Performances of four randomization methods without early stopping for the horizon size N = 1000 as assessed by the mean proportion in arm 2 (the superior treatment), mean overall response rate at the horizon level, and power at the trial level, with θ₁ = 0.2 and θ₂ = 0.2, 0.4, and 0.6, respectively. On the horizontal axis, m represents the trial size. The red line represents the BAR design, and orange, green, and black lines represent SML, SPM and ER, respectively. Each line was derived from 100,000 simulations. The tuning parameter λ was specified as 1.

Figure 3

Performances of four randomization methods without early stopping for the horizon size N = 50, 000 as assessed by the mean proportion in arm 2 (the superior treatment), mean overall response rate at the horizon level, and power at the trial level, with θ₁ = 0.2 and θ₂ = 0.2, 0.4, and 0.6, respectively. On the horizontal axis, m represents the trial size. The red line represents the BAR design, and orange, green, and black lines represent SML, SPM and ER, respectively. Each line was derived from 100,000 simulations. The tuning parameter λ was specified as 1.

Figure 4

Performances of four randomization methods with early stopping for the horizon size N = 1, 000 as assessed by the mean proportion in arm 2 (the superior treatment), mean overall response rate at the horizon level, power, and mean trial size at the trial level, with θ₁ = 0.2 and θ₂ = 0.2, 0.4, and 0.6, respectively. On the horizontal axis, m represents the trial size. The red line represents the BAR design, and orange, green, and black lines represent SML, SPM and ER, respectively. Each line was derived from 100,000 simulations. The tuning parameter λ was specified as 1.

Figure 5

Performances of four randomization methods with early stopping for the horizon size N = 50, 000 as assessed by the mean proportion in arm 2 (the superior treatment), mean overall response rate at the horizon level, power, and mean trial size at the trial level, with θ₁ = 0.2 and θ₂ = 0.2, 0.4, and 0.6, respectively. On the horizontal axis, m represents the trial size. The red line represents the BAR design, and orange, green, and black lines represent SML, SPM and ER, respectively. Each line was derived from 100,000 simulations. The tuning parameter λ was specified as 1.