Bayesian inference of sampled ancestor trees for epidemiology and fossil calibration
- PMID: 25474353
- PMCID: PMC4263412
- DOI: 10.1371/journal.pcbi.1003919
Bayesian inference of sampled ancestor trees for epidemiology and fossil calibration
Abstract
Phylogenetic analyses which include fossils or molecular sequences that are sampled through time require models that allow one sample to be a direct ancestor of another sample. As previously available phylogenetic inference tools assume that all samples are tips, they do not allow for this possibility. We have developed and implemented a Bayesian Markov Chain Monte Carlo (MCMC) algorithm to infer what we call sampled ancestor trees, that is, trees in which sampled individuals can be direct ancestors of other sampled individuals. We use a family of birth-death models where individuals may remain in the tree process after sampling, in particular we extend the birth-death skyline model [Stadler et al., 2013] to sampled ancestor trees. This method allows the detection of sampled ancestors as well as estimation of the probability that an individual will be removed from the process when it is sampled. We show that even if sampled ancestors are not of specific interest in an analysis, failing to account for them leads to significant bias in parameter estimates. We also show that sampled ancestor birth-death models where every sample comes from a different time point are non-identifiable and thus require one parameter to be known in order to infer other parameters. We apply our phylogenetic inference accounting for sampled ancestors to epidemiological data, where the possibility of sampled ancestors enables us to identify individuals that infected other individuals after being sampled and to infer fundamental epidemiological parameters. We also apply the method to infer divergence times and diversification rates when fossils are included along with extant species samples, so that fossilisation events are modelled as a part of the tree branching process. Such modelling has many advantages as argued in the literature. The sampler is available as an open-source BEAST2 package (https://github.com/CompEvol/sampled-ancestors).
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures

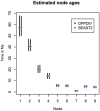
 , where
, where  denotes the ranked tree topology and
denotes the ranked tree topology and  ,
,  , and
, and  denote the node ages. In the reconstructed tree the root is a sampled node. In the skyline model, birth-death parameters vary from interval to interval. There are two intervals in this figure bounded by the time of origin
denote the node ages. In the reconstructed tree the root is a sampled node. In the skyline model, birth-death parameters vary from interval to interval. There are two intervals in this figure bounded by the time of origin  , parameter shift time
, parameter shift time  , and present time
, and present time  . Between
. Between  and
and  parameters
parameters  ,
,  ,
,  and
and  apply and between
apply and between  and
and  parameters
parameters  ,
,  ,
,  , and
, and  . There are additional sampling attempts at times
. There are additional sampling attempts at times  and
and  with sampling probabilities
with sampling probabilities  and
and  .
.
 (blue edge) either from a branch, coloured black, in case a.1 or from a node, coloured black, in case a.2. Then it attaches the subtree either to an edge
(blue edge) either from a branch, coloured black, in case a.1 or from a node, coloured black, in case a.2. Then it attaches the subtree either to an edge  (black edge) at a random height in case b.1 or to a leaf
(black edge) at a random height in case b.1 or to a leaf  (black node) in case b.2. Case a.1 followed by b.2 removes a node from the tree and case a.2 followed by b.1 introduces a new node into the tree.
(black node) in case b.2. Case a.1 followed by b.2 removes a node from the tree and case a.2 followed by b.1 introduces a new node into the tree.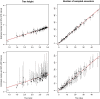

 , against tree sizes for simulated fossilized birth-death process. The black dots are the interval widths for posterior distributions obtained from the analyses of simulated sequence data of all sampled nodes and the red triangles are the interval widths from the analyses of sequence data of only extant samples.
, against tree sizes for simulated fossilized birth-death process. The black dots are the interval widths for posterior distributions obtained from the analyses of simulated sequence data of all sampled nodes and the red triangles are the interval widths from the analyses of sequence data of only extant samples.
 , (on the left) and removal probability,
, (on the left) and removal probability,  , (on the right).
, (on the right).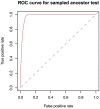

References
-
- Yang Z, Rannala B (1997) Bayesian phylogenetic inference using DNA sequences: a Markov chain Monte Carlo method. Mol Biol Evol 14: 717–24. - PubMed
-
- Mau B, Newton MA, Larget B (1999) Bayesian phylogenetic inference via Markov chain Monte Carlo methods. Biometrics 55: 1–12. - PubMed
-
- Huelsenbeck JP, Ronquist F (2001) MRBAYES: Bayesian inference of phylogenetic trees. Bioinformatics 17: 754–755. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials
Miscellaneous

