Non-adiabatic dynamics close to conical intersections and the surface hopping perspective

Abstract

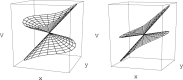
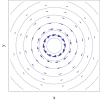
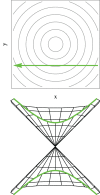
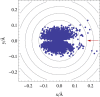
Conical intersections play a major role in the current understanding of electronic de-excitation in polyatomic molecules, and thus in the description of photochemistry and photophysics of molecular systems. This article reviews aspects of the basic theory underlying the description of non-adiabatic transitions at conical intersections, with particular emphasis on the important case when the dynamics of the nuclei are treated classically. Within this classical nuclear motion framework, the main aspects of the surface hopping methodology in the conical intersection context are presented. The emerging picture from this treatment is that of electronic transitions around conical intersections dominated by the interplay of the nuclear velocity and the derivative non-adiabatic coupling vector field.

Keywords: Born-Oppenheimer approximation; Landau-Zener; conical intersections; decoherence; non-adiabatic dynamics; surface hopping.

Figure 1

Electronic energy surfaces form in the vicinity of two generic conical intersections as given by Equation (32) [or equivalently by Equation (33)]. On the left panel the tilt angle α_x in Equation (33) is equal to 10° and the conical intersection corresponds to a local minimum of the upper state electronic energy surface (peaked intersection, Atchity et al., 1991). On the right panel α_x = 50°, the conical intersection in no longer a local energy minimum (sloped intersection, Atchity et al., 1991).

Figure 2

Representation of the derivative non-adiabatic coupling vector field, given by Equation (45), in the vicinity of a conical intersection described by Equation (33), with the apex at the center and α_x = α_y = 0 and e = 1. Contour lines represent the electronic eigenstate energy gap and the arrow size is proportional to the magnitude of non-adiabatic coupling vectors.

Figure 3

Absolute value of the inner product of the derivative non-adiabatic coupling vector field (white arrows) in the vicinity of a conical intersection given by Equation (33), with the apex at the center and α_x = α_y = 0 and e = 1, with a uniform nuclear velocity with no component along the y axis (red arrows). Brighter color represents higher inner product magnitude. Contour lines represent the electronic eigenstate energy gap, with the conical intersection located at the center of the plot.

Figure 4

Energy profiles of the diagonal elements of the diabatic (- -) and adiabatic (–) matrices Equation (58) for the LZ model as a function of the nuclear trajectory length z(t). z_c corresponds to the configuration along the trajectory for which the diabatic states are degenerate and where the energy gap between adiabatic states is minimal. Geometrically the adiabatic curves are hyperbolas and the diabatic curves correspond to their asymptotes. The left hand side panel presents a case where the diabatic state energy variations with z(t) have slopes of different sign, while on the right hand side both slopes are negative.

Figure 5

The adiabatic potential energy profile for a straight line trajectory on the branching space for potential energy surfaces given by Equation (32) [or equivalently by Equation (33)] is hyperbolic. The upper panel represents the straight line trajectory in the branching plane in the vicinity of the conical intersection, while the lower panel represents a vertical cut on the double cone potential highlighting the hyperbolic profile.

Figure 6

Position where hops from the upper to the lower surface occur in a fewest switches surface hopping simulation near a conical intersection given by Equation (33). The initial distribution of trajectories has a gaussian distribution along the y axis with a standard deviation of 0.04 Å, and are started with a velocity only along x (see Appendix Section Simulation Details). The red arrow indicates the direction of the incoming distribution of classical trajectories and the contour lines represent energy contours for the upper surface (or the electronic eigenstate energy gap).

Figure 7

Upper state population evolution in a fewest switches simulation of an initial gaussian distribution of trajectories in a double cone potential given by Equation (33). Represented are the square of the modulus of the excited electronic eigenstate component of the time dependent electronic state which is propagated in time through Equation (75), and the fraction of trajectories propagated on the upper state surface (P₊). Also represented is the cumulative number of frustrated hops normalized by the total number of trajectories.

Figure 8

Comparison of the evolution of the system in a surface hopping scheme with the trajectory propagated on the lower potential energy surface (left panel) and a system with quantum mechanical nuclear motion (right panel). It is crucial to note that in the fewest switches scheme, although the trajectory is being propagated on the lower surface (in this example), it can be seen as being followed by a “ghost” trajectory on the upper state associated with the coefficient 〈ϕ₂; $\overrightarrow{R}$|Φ; $\overrightarrow{R}$〉. These coefficients are propagated in time through Equation (75) and in a conventional fewest switches scheme are not reset after a hop. Nuclear wavefunctions 〈$\overrightarrow{R}$, ϕ₁; $\overrightarrow{R}$|Ψ〉 and 〈$\overrightarrow{R}$, ϕ₂; $\overrightarrow{R}$|Ψ〉 associated with different states will evolve to explore different regions of nuclear position space.