Reliable estimation of prediction errors for QSAR models under model uncertainty using double cross-validation
- PMID: 25506400
- PMCID: PMC4260165
- DOI: 10.1186/s13321-014-0047-1
Reliable estimation of prediction errors for QSAR models under model uncertainty using double cross-validation
Abstract
Background: Generally, QSAR modelling requires both model selection and validation since there is no a priori knowledge about the optimal QSAR model. Prediction errors (PE) are frequently used to select and to assess the models under study. Reliable estimation of prediction errors is challenging - especially under model uncertainty - and requires independent test objects. These test objects must not be involved in model building nor in model selection. Double cross-validation, sometimes also termed nested cross-validation, offers an attractive possibility to generate test data and to select QSAR models since it uses the data very efficiently. Nevertheless, there is a controversy in the literature with respect to the reliability of double cross-validation under model uncertainty. Moreover, systematic studies investigating the adequate parameterization of double cross-validation are still missing. Here, the cross-validation design in the inner loop and the influence of the test set size in the outer loop is systematically studied for regression models in combination with variable selection.
Methods: Simulated and real data are analysed with double cross-validation to identify important factors for the resulting model quality. For the simulated data, a bias-variance decomposition is provided.
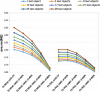
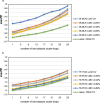
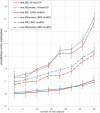
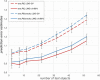
Results: The prediction errors of QSAR/QSPR regression models in combination with variable selection depend to a large degree on the parameterization of double cross-validation. While the parameters for the inner loop of double cross-validation mainly influence bias and variance of the resulting models, the parameters for the outer loop mainly influence the variability of the resulting prediction error estimate.
Conclusions: Double cross-validation reliably and unbiasedly estimates prediction errors under model uncertainty for regression models. As compared to a single test set, double cross-validation provided a more realistic picture of model quality and should be preferred over a single test set.
Keywords: Cross-validation; Double cross-validation; External validation; Internal validation; Prediction error; Regression.
Figures




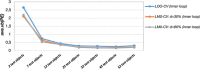
References
-
- Kubinyi H. QSAR and 3D QSAR in drug design. Part 1: methodology. Drug Discov Today. 1997;2:457–467. doi: 10.1016/S1359-6446(97)01079-9. - DOI
-
- Baumann K. Cross-validation as the objective function of variable selection. Trends Anal Chem. 2003;22:395–406. doi: 10.1016/S0165-9936(03)00607-1. - DOI
-
- Todeschini R, Consonni V. Handbook of Molecular Descriptors. Berlin: Wiley-VCH; 2002.
-
- Hastie T, Tibshirani R, Friedmann J. Elements of statistical Learning: Data Mining, Inference and Prediction. 2. New York: Springer; 2009.
-
- Mosteller F, Turkey J. Data Analysis, Including Statistics. In: Gardner L, Eliot A, editors. The Handbook of Social Psychology. 2. Springer: Addison-Wesley, Reading, MA, USA; 1968. pp. 109–112.
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials

