Ultra-responsive soft matter from strain-stiffening hydrogels

Abstract

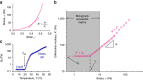
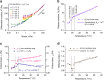
The stiffness of hydrogels is crucial for their application. Nature's hydrogels become stiffer as they are strained. This stiffness is not constant but increases when the gel is strained. This stiffening is used, for instance, by cells that actively strain their environment to modulate their function. When optimized, such strain-stiffening materials become extremely sensitive and very responsive to stress. Strain stiffening, however, is unexplored in synthetic gels since the structural design parameters are unknown. Here we uncover how readily tuneable parameters such as concentration, temperature and polymer length impact the stiffening behaviour. Our work also reveals the marginal point, a well-described but never observed, critical point in the gelation process. Around this point, we observe a transition from a low-viscous liquid to an elastic gel upon applying minute stresses. Our experimental work in combination with network theory yields universal design principles for future strain-stiffening materials.

Figure 1. Ethylene glycol substituted polyisocyanopeptides.

Molecular structure of the tri(ethylene glycol)-substituted polyisocyanopeptides. In purple the polymer backbone of 270–1,430 repeat units. Every carbon atom holds a substituent, composed of a dipeptide (Ala–Ala, red) and a short methyl-terminated tri(ethylene glycol) tail (blue).

Figure 2. Strain stiffening of a polyisocyanopeptide hydrogel.

(a) Stress-strain curve of polymer P1f (1 mg ml⁻¹, T=37 °C) in a stress ramp. (b) The stiffness represented as the differential modulus K′≡δσ/δγ as a function of stress σ for the same polymer. At low stress, K′=G₀ the plateau modulus, but beyond a critical stress σ_c, K′ increases, following K′∝σ^m where the exponent m is the stiffening index. (c) The thermally induced gelation process is unmistakably observed by plotting G₀ versus temperature T. We define the gel point as the onset of modulus increase, here at 19 °C.

Figure 3. Mechanical properties of PIC hydrogels (P1f, T=25 °C) as a function of polymer concentration.

(a) Differential modulus against stress at different polymer concentrations. Note that the y-axis spans 3 orders of magnitude in stiffness with a concentration range of only 1 order of magnitude. The dashed red line at σ=10 Pa indicates where m was determined. (b) Plateau modulus G₀ (orange) and critical stress σ_c (dark red) against concentration (c). The solid lines are power law fits and show that both scale with c^2.0. (c) Scaling K′ with G₀ and σ with σ_c causes a collapse of the data to a single master curve that shows K′∝σ^3/2 only at high σ. The blue dashed line shows the point close to σ_c where m was determined. (d) Stiffening index m as a function of concentration. When determined close to σ_c (blue squares), m is similar for all concentrations; when determined at a given stress (red circles, σ=10 Pa), m is higher for lower concentration gels (since at lower c, σ_c is much lower and thus σ–σ_c will be higher). Note that the concentration axes (b,d) have logarithmic scales.

Figure 4. Molecular weight dependence of the mechanical properties of the P1b–P1g hydrogels (at c=1 mg ml⁻¹).

(a) Differential modulus against stress for different molecular weight or length L polymers at T=37 °C. The solid line shows the high stress limit m=3/2. (b) Plateau modulus G₀ as a function of temperature for gels of different length polymers. (c) Data extracted from b: G₀ as a function of L at T=37, 45 and 55 °C. The solid line shows quadratic fits to (L–L_min), where fitting parameter L_min represents a minimum polymer length (see main text). (d) The critical stress σ_c as a function of L at the same temperature. Here the solid lines are linear fits to (L–L_min).

Figure 5. Temperature dependence of the mechanical properties of the P1f hydrogel (at 1 mg ml^–1).

(a) Differential modulus against stress at different temperatures. The solid line shows the high stress limit m=3/2. (b) Plateau modulus G₀, as a function of temperature T (linear scale). In the gel at T≥22 °C, G₀ increases exponentially with T over the investigated temperature window; the solid line is a fit to Te^2βT with β≈0.08 K⁻¹. At T≤22 °C, G₀ increases fast with T, corresponding to the transition from liquid to gel. (c) critical stress σ_c (pink circles) and critical strain γ_c (blue squares) as a function of T; the solid lines are fits to Te^βT and e^−βT with β≈0.08 K⁻¹. Both σ_c and γ_c show a sharp decrease at T≤22 °C. (d) The stiffening index m as a function of T clearly shows three regimes. In the high temperature regime, m weakly scales linearly with T, and around the marginal regime (see text) m sharply decreases while it restores to 0.9 on further decreasing T. The values for m were recorded at stresses close to the critical stress (at σ=3σ_c). At higher stress, in particular at high temperature, m will approach 1.5 ref. , but such stresses are impossible to apply close to T_gel.

Figure 6. Interpolated mechanical properties of gels with constant modulus and varying sensitivity to stress.

When in a series of gels the product L × c and G₀ remain constant, but σ_c changes. Here we selected four series of constant G₀ in the range 10–1,000 Pa (squares) and σ_c varying in each series (circles). The projection of the curves on the x–y plane (dashed lines) shows the corresponding length and concentrations.