Correcting Duporcq's theorem

Abstract

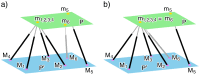
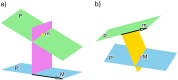
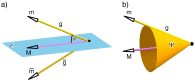
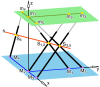
In 1898, Ernest Duporcq stated a famous theorem about rigid-body motions with spherical trajectories, without giving a rigorous proof. Today, this theorem is again of interest, as it is strongly connected with the topic of self-motions of planar Stewart-Gough platforms. We discuss Duporcq's theorem from this point of view and demonstrate that it is not correct. Moreover, we also present a revised version of this theorem.

Keywords: Architectural singularity; Borel Bricard problem; Self-motion; Stewart–Gough platform.

Fig. 1

a) Sketch of the cubics Γ₃ and Γ₄ and their intersection points 1, …, 6, α, β, γ. b) It is well known (cf. page 166 of [10]), that the bisecting planes ε_i of corresponding points a₁ ∈ P₁ and a_i ∈ P_i are related with the midpoints b_i of the segment a₁a_i by a null-polarity (for i = 2, 3). Therefore, the mapping from a ∈ P to the intersection line A_i of ε_i an P′ is a correlation. The intersection point of A₂ and A₃ is equivalent with the intersection point of the axis of the circumcircle of a₁, a₂, a₃ and P′.

Fig. 2

a) A planar architecturally singular SG platform is given, where the platform anchor points m_i and the base anchor points M_i are related by a non-singular projectivity κ; i.e. m_iκ = M_i for i = 1, …, 6 (cf. Theorem 2). b) It is well known (e.g. Section 3.1 of [12]), that planar architecturally singular SG platforms are redundant. Therefore they possess a self-motion in each pose. It can easily be seen by the above given example, that this only holds over ℂ: In the illustrated pose the platform and the base coincide as well as the centers of the two circles c and cκ (κ is a similarity).

Fig. 3

Given is a 5-legged manipulator with m_1,2,3,4 := m₁ = m₂ = m₃ = m₄. This manipulator is degenerated (cf. [14]) and possess a two-parametric spherical self-motion with center m_1,2,3,4. By adding any leg with anchor points m₆ ∈ P and M₆ ∈ P′, we always obtain a planar architecturally singular SG platform: a) In the general case, the sixth leg restricts the self-motion to a one-dimensional one. b) If we choose m₆ = m_1,2,3,4, the resulting SG platform has the same solution for the direct kinematics as the given 5-legged one.

Fig. 4

a) Sketch of the Darboux condition. b) Sketch of the Mannheim condition.

Fig. 5

a) The reflection of m, with respect to an finite plane ε through M, can easily be done by considering m as the ideal point of a line g. Then the reflected point $\overline{\mathrm{m}}$ is the ideal point of the reflected line $\overline{\mathrm{g}}$ with respect to ε. b) The obtained set of points $\overline{\mathrm{m}}$ are the ideal points of a cone of revolution Ψ with half apex angle φ and where M is located on the axis of revolution.

Fig. 6

Special case: a) Sketch of the platform. b) Sketch of the base.

Fig. 7

Axonometric view of the 5-legged manipulator in its initial pose.