Optimal inference with suboptimal models: addiction and active Bayesian inference
- PMID: 25561321
- PMCID: PMC4312353
- DOI: 10.1016/j.mehy.2014.12.007
Optimal inference with suboptimal models: addiction and active Bayesian inference
Erratum in
-
Corrigendum to 'Optimal inference with suboptimal models: Addiction and active Bayesian inference' [Med. Hypotheses 84 (2015) 109-117].Med Hypotheses. 2016 Jun;91:123. doi: 10.1016/j.mehy.2016.02.021. Epub 2016 Mar 7. Med Hypotheses. 2016. PMID: 27142158 Free PMC article. No abstract available.
Abstract
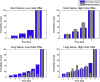
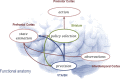
When casting behaviour as active (Bayesian) inference, optimal inference is defined with respect to an agent's beliefs - based on its generative model of the world. This contrasts with normative accounts of choice behaviour, in which optimal actions are considered in relation to the true structure of the environment - as opposed to the agent's beliefs about worldly states (or the task). This distinction shifts an understanding of suboptimal or pathological behaviour away from aberrant inference as such, to understanding the prior beliefs of a subject that cause them to behave less 'optimally' than our prior beliefs suggest they should behave. Put simply, suboptimal or pathological behaviour does not speak against understanding behaviour in terms of (Bayes optimal) inference, but rather calls for a more refined understanding of the subject's generative model upon which their (optimal) Bayesian inference is based. Here, we discuss this fundamental distinction and its implications for understanding optimality, bounded rationality and pathological (choice) behaviour. We illustrate our argument using addictive choice behaviour in a recently described 'limited offer' task. Our simulations of pathological choices and addictive behaviour also generate some clear hypotheses, which we hope to pursue in ongoing empirical work.
Copyright © 2014 The Authors. Published by Elsevier Ltd.. All rights reserved.
Figures




Similar articles
-
The anatomy of choice: dopamine and decision-making.Philos Trans R Soc Lond B Biol Sci. 2014 Nov 5;369(1655):20130481. doi: 10.1098/rstb.2013.0481. Philos Trans R Soc Lond B Biol Sci. 2014. PMID: 25267823 Free PMC article.
-
Active inference and epistemic value.Cogn Neurosci. 2015;6(4):187-214. doi: 10.1080/17588928.2015.1020053. Epub 2015 Mar 13. Cogn Neurosci. 2015. PMID: 25689102
-
Modeling other minds: Bayesian inference explains human choices in group decision-making.Sci Adv. 2019 Nov 27;5(11):eaax8783. doi: 10.1126/sciadv.aax8783. eCollection 2019 Nov. Sci Adv. 2019. PMID: 31807706 Free PMC article. Clinical Trial.
-
An evolutionary perspective on information processing.Top Cogn Sci. 2014 Apr;6(2):312-30. doi: 10.1111/tops.12085. Epub 2014 Mar 11. Top Cogn Sci. 2014. PMID: 24616372 Review.
-
A unified framework for addiction: vulnerabilities in the decision process.Behav Brain Sci. 2008 Aug;31(4):415-37; discussion 437-87. doi: 10.1017/S0140525X0800472X. Behav Brain Sci. 2008. PMID: 18662461 Free PMC article. Review.
Cited by
-
Computational Phenotyping in Psychiatry: A Worked Example.eNeuro. 2016 Aug 2;3(4):ENEURO.0049-16.2016. doi: 10.1523/ENEURO.0049-16.2016. eCollection 2016 Jul-Aug. eNeuro. 2016. PMID: 27517087 Free PMC article.
-
Human confidence judgments reflect reliability-based hierarchical integration of contextual information.Nat Commun. 2019 Nov 28;10(1):5430. doi: 10.1038/s41467-019-13472-z. Nat Commun. 2019. PMID: 31780659 Free PMC article.
-
Computational analysis of probabilistic reversal learning deficits in male subjects with alcohol use disorder.Front Psychiatry. 2022 Oct 19;13:960238. doi: 10.3389/fpsyt.2022.960238. eCollection 2022. Front Psychiatry. 2022. PMID: 36339830 Free PMC article.
-
Computational Neuropsychology and Bayesian Inference.Front Hum Neurosci. 2018 Feb 23;12:61. doi: 10.3389/fnhum.2018.00061. eCollection 2018. Front Hum Neurosci. 2018. PMID: 29527157 Free PMC article. Review.
-
Scene Construction, Visual Foraging, and Active Inference.Front Comput Neurosci. 2016 Jun 14;10:56. doi: 10.3389/fncom.2016.00056. eCollection 2016. Front Comput Neurosci. 2016. PMID: 27378899 Free PMC article.
References
-
- Bechara A. Decision making, impulse control and loss of willpower to resist drugs: a neurocognitive perspective. Nat. Neurosci. 2005;8(11):1458–1463. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

