Dynamics of actin waves on patterned substrates: a quantitative analysis of circular dorsal ruffles
- PMID: 25574668
- PMCID: PMC4289068
- DOI: 10.1371/journal.pone.0115857
Dynamics of actin waves on patterned substrates: a quantitative analysis of circular dorsal ruffles
Erratum in
-
Correction: Dynamics of actin waves on patterned substrates: a quantitative analysis of circular dorsal ruffles.PLoS One. 2015 Mar 25;10(3):e0119746. doi: 10.1371/journal.pone.0119746. eCollection 2015. PLoS One. 2015. PMID: 25807117 Free PMC article. No abstract available.
Abstract
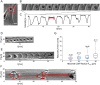
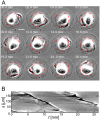
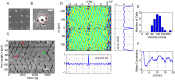
Circular Dorsal Ruffles (CDRs) have been known for decades, but the mechanism that organizes these actin waves remains unclear. In this article we systematically analyze the dynamics of CDRs on fibroblasts with respect to characteristics of current models of actin waves. We studied CDRs on heterogeneously shaped cells and on cells that we forced into disk-like morphology. We show that CDRs exhibit phenomena such as periodic cycles of formation, spiral patterns, and mutual wave annihilations that are in accord with an active medium description of CDRs. On cells of controlled morphologies, CDRs exhibit extremely regular patterns of repeated wave formation and propagation, whereas on random-shaped cells the dynamics seem to be dominated by the limited availability of a reactive species. We show that theoretical models of reaction-diffusion type incorporating conserved species capture partially the behavior we observe in our data.
Conflict of interest statement
Figures



References
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources

