Evolution and emergence of infectious diseases in theoretical and real-world networks
- PMID: 25592476
- PMCID: PMC4335509
- DOI: 10.1038/ncomms7101
Evolution and emergence of infectious diseases in theoretical and real-world networks
Abstract
One of the most important advancements in theoretical epidemiology has been the development of methods that account for realistic host population structure. The central finding is that heterogeneity in contact networks, such as the presence of 'superspreaders', accelerates infectious disease spread in real epidemics. Disease control is also complicated by the continuous evolution of pathogens in response to changing environments and medical interventions. It remains unclear, however, how population structure influences these adaptive processes. Here we examine the evolution of infectious disease in empirical and theoretical networks. We show that the heterogeneity in contact structure, which facilitates the spread of a single disease, surprisingly renders a resident strain more resilient to invasion by new variants. Our results suggest that many host contact structures suppress invasion of new strains and may slow disease adaptation. These findings are important to the natural history of disease evolution and the spread of drug-resistant strains.
Figures
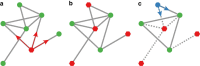

 . (g) The selection exponent, α, is calculated by fitting Pfix versus r to equation (27). Lower values mean that selection is suppressed compared to the uniform network. For a uniform or well-mixed population we expect α=1. Fits are shown by the solid lines in panels (d) and (f).
. (g) The selection exponent, α, is calculated by fitting Pfix versus r to equation (27). Lower values mean that selection is suppressed compared to the uniform network. For a uniform or well-mixed population we expect α=1. Fits are shown by the solid lines in panels (d) and (f).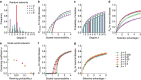
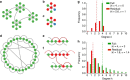
References
-
- Anderson R. & May R. Infectious Diseases of Humans: Dynamics and Control Oxford University Press (1991).
-
- Watts D. J. & Strogatz S. H. Collective dynamics of ‘small-world’ networks. Nature 393, 440–442 (1998). - PubMed
-
- May R. M. & Lloyd A. L. Infection dynamics on scale-free networks. Phys. Rev. E 64, 066112 (2001). - PubMed
-
- Pastor-Satorras R. & Vespignani A. Epidemic dynamics and endemic states in complex networks. Phys. Rev. E 63, 066117 (2001a). - PubMed
-
- Newman M. E. J. Spread of epidemic disease on networks. Phys. Rev. E 66, 016128 (2002). - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

