Motion artifacts in MRI: A complex problem with many partial solutions

Abstract

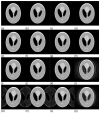
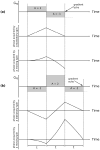
Subject motion during magnetic resonance imaging (MRI) has been problematic since its introduction as a clinical imaging modality. While sensitivity to particle motion or blood flow can be used to provide useful image contrast, bulk motion presents a considerable problem in the majority of clinical applications. It is one of the most frequent sources of artifacts. Over 30 years of research have produced numerous methods to mitigate or correct for motion artifacts, but no single method can be applied in all imaging situations. Instead, a "toolbox" of methods exists, where each tool is suitable for some tasks, but not for others. This article reviews the origins of motion artifacts and presents current mitigation and correction methods. In some imaging situations, the currently available motion correction tools are highly effective; in other cases, appropriate tools still need to be developed. It seems likely that this multifaceted approach will be what eventually solves the motion sensitivity problem in MRI, rather than a single solution that is effective in all situations. This review places a strong emphasis on explaining the physics behind the occurrence of such artifacts, with the aim of aiding artifact detection and mitigation in particular clinical situations.

Keywords: MRI; motion artifact; motion correction; motion prevention; review.

Fig. 1

(a) Original FFT reconstruction without motion, (b-d) sum of first and last source images to show the range of simulated motions for (b) continuous monotonic rotation to the total angle of 10°, (c) continuous vertical translation and (d) continuous horizontal translation (in both cases 10 pixels for a matrix of 256×256). Periodic horizontal translation has the same amplitude and is not shown. Images (e-h) demonstrate the results of averaging the motion as would correspond to photography with an equivalently long exposure time; (e) rotation, (f) vertical translation, (g) horizontal translation and (h) periodic horizontal translation. Note the loss of detail and edge information due to the motion blur and the enhanced blurring in (h) due to the fact that with sinusoidal motion the object spends more time close to the terminal positions. Images (i-l) show simulated MRI acquisitions with linear k-space ordering. Images (m-p) show simulated two-shot interleaved MRI acquisitions. Plots of the motion as a function of k-space position for the representative images are presented in Fig. 2.

Fig. 2

Effective translation (as a fraction of the FOV) as a function of the k-space position for (a) Fig. 1j and 1k, (b) Fig. 1l, (c) Fig. 1n and 1o and (d) Fig. 1p. As seen, if the external disturbance oscillates as a function of k-space position, e g. in cases (b), (c) and (d), ghosting will result (see corresponding images in Fig. 1). Reduced ghosting in Fig. 1p can be explained by the effective reduced frequency of oscillation of the position as a function of the k-space coordinate (compare plots (b) and (d)). Plots of rotations are omitted due to their similar appearance.

Fig. 3

Simulations of a single sudden orientation change during the k-space acquisition for different k-space acquisition strategies and different amounts of inconsistent k-space data. For a linear k-space ordering, images reconstructed from datasets containing (a) 12.5%, (b) 25%, (c) 37.5% and (d) 50% inconsistent data have been simulated. Hardly any artefacts are visible if the corruption occurs outside of the ½ of the maximum k-space distance to the centre. Similar conclusions follow for the two-shot interleaved k-space acquisitions with (e) 12.5%, (f) 25%, (g) 37.5% and (h) 50% of inconsistent data. Images (i-l) present a similar simulation for the centric reordering with (i) 50% of inconsistent with respect to the k-space centre data, (j) 62.5%, (k) 75% and (l) 87.5%, respectively. The precise threshold at which visually detectable artefacts start to appear strongly depends on the image, primarily on the presence of small high-contrast features, but the overall tendency is that below a certain distance from the k-space centre a single motion event produces only negligible artefacts.

Fig. 4

Velocity effects on the phase of MR signals. Stationary spins can be refocused with a pair of gradient pulses of equal area and opposite polarity, which is a basis of gradient echo. Spins moving along the gradient direction acquire additional phase due to the fact that dephasing and refocusing occur at different physical locations where the same gradient indices different frequency shifts, leading to different amounts of the phase acquired during dephasing and refocusing periods. Greyed segments on the corresponding phase circles mark the amount of phase acquired by the moving spins during the last gradient pulse.

Fig. 5

Excitation history effects visualized for a 3-pulse MR pulse sequence. In the case of no motion, regions excited by all three pulses overlap resulting in the desired signal evolution. The respective brain regions are marked using half-transparent bands with the colour of the corresponding slice-selective RF pulse. Overlap of red and green results in light brown. When light brown is followed by an overlap with blue, a grey colour results, which indicates the desired spin evolution. In the case of motion, (rotation after the first pulse, followed by a combination of rotation and translation after the second pulse, original position is shown as dotted line) the grey region corresponding to the desired spin evolution is substantially reduced, while coloured regions with undesired signal evolution appear. Therefore desired signals are decreased, and undesired signals are produced, resulting in artefacts, such as ghosting or signal disturbances. The unwanted signals may also cancel some of the desired signals, causing signal voids.

Fig. 6

The effect of rotations on the k-space sample locations in object coordinates. In the absence of rotations (a) the k-space samples are arranged on a uniform grid fulfilling the Nyquist criterion. Rotation of the object during the image acquisition rotates the spatial frequency components associated with the object with respect to the encoding gradients, which effectively redistributes the samples in k-space (b). This leads the sampling density in some areas of k-space to fall below the Nyquist criterion and results in streaking and ghosting artefacts in the images, which are difficult to correct for in reconstruction even if the motion is known.

Fig. 7

The effect of linear motion on the phase acquired by the spins under the action of the encoding gradients (frequency encoding in this example). A bipolar gradient (a) refocuses the stationary spins at the moment when the net area under the gradient arrives to zero. This is because the phase accrual in this case is proportional to a product of the gradient amplitude and the time duration. Contrary to that, the phase acquired by a spin moving along the gradient direction is proportional to the gradient amplitude, duration and the displacement of the spin. Because the displacement under the continuous motion is proportional to the time, the phase shows a quadratic dependency on time. Therefore, a bipolar gradient fails to refocus moving spins. Consequently, such spins will be poorly located and a motion artefact will be seen in vascular structures and moving fluids. It is possible to account for the quadratic behaviour of the phase by introducing a third gradient lobe, as shown in (b). Here, in order to keep the polarity of the frequency encoding gradient the sign of the two preceding lobes has been adjusted. The gradient area ratio of 1:-2:1 does not induce additional dephasing for the stationary spins and allows for refocusing the spins moving with a constant velocity. Other gradient schemes are possible taking into account gradient amplitude and slew rate limits, but velocity compensation always increases the minimal echo time.