Optimal Lévy-flight foraging in a finite landscape
- PMID: 25631566
- PMCID: PMC4345481
- DOI: 10.1098/rsif.2014.1158
Optimal Lévy-flight foraging in a finite landscape
Abstract
We present a simple model to study Lévy-flight foraging with a power-law step-size distribution [P(l) ∞ l-μ] in a finite landscape with countable targets. We find that different optimal foraging strategies characterized by a wide range of power-law exponent μopt, from ballistic motion (μopt → 1) to Lévy flight (1 < μopt < 3) to Brownian motion (μopt ≥ 3), may arise in adaptation to the interplay between the termination of foraging, which is regulated by the number of foraging steps, and the environmental context of the landscape, namely the landscape size and number of targets. We further demonstrate that stochastic returning can be another significant factor that affects the foraging efficiency and optimality of foraging strategy. Our study provides a new perspective on Lévy-flight foraging, opens new avenues for investigating the interaction between foraging dynamics and the environment and offers a realistic framework for analysing animal movement patterns from empirical data.
Keywords: Lévy flight; optimal foraging; random search.
Figures
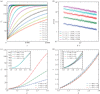
 versus the number of undiscovered targets K − S. The dots represent simulation results, and the lines represent the corresponding linear regression fit. (c) The mean number of steps between two consecutive detections nd as a function of μ for different values of L and K. Here, K is adjusted to obtain the corresponding λ given L. The solid lines represent the nonlinear fitting
versus the number of undiscovered targets K − S. The dots represent simulation results, and the lines represent the corresponding linear regression fit. (c) The mean number of steps between two consecutive detections nd as a function of μ for different values of L and K. Here, K is adjusted to obtain the corresponding λ given L. The solid lines represent the nonlinear fitting  . (d) The constant coefficient γ as a function of μ for different values of L and K. The solid lines represent the cubic polynomial fitting.
. (d) The constant coefficient γ as a function of μ for different values of L and K. The solid lines represent the cubic polynomial fitting.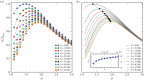

 from numerical simulation with the intensity of stochastic returning β = 0, the landscape size L = 1000, the number of targets K = 5000 and the termination condition
from numerical simulation with the intensity of stochastic returning β = 0, the landscape size L = 1000, the number of targets K = 5000 and the termination condition  where
where  is the accumulated moving distance. The results are averaged over 100 realizations. (b) η evaluated by the mean-field solution by setting the total number of steps N by
is the accumulated moving distance. The results are averaged over 100 realizations. (b) η evaluated by the mean-field solution by setting the total number of steps N by  in equation (3.3).
in equation (3.3).
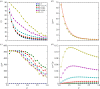
 versus the power-law exponent μ. (b) The mean step-size in exploration
versus the power-law exponent μ. (b) The mean step-size in exploration  versus μ. The red solid line represents equation (3.4). (c) The mean step-size in return
versus μ. The red solid line represents equation (3.4). (c) The mean step-size in return  versus μ. (d) The ratio of the number of return steps Nret to the total number of steps N versus μ. In panels (a–d), the dots represent simulations results, and the dashed lines are a guide to the eye. Different colours correspond to different values of β, as indicated in the legend of panel (a). The results are obtained from numerical simulation with the landscape size L = 1000, the number of targets K = 5000 and the termination condition Θn = δ(n − 50 000) and are averaged over 100 realizations.
versus μ. (d) The ratio of the number of return steps Nret to the total number of steps N versus μ. In panels (a–d), the dots represent simulations results, and the dashed lines are a guide to the eye. Different colours correspond to different values of β, as indicated in the legend of panel (a). The results are obtained from numerical simulation with the landscape size L = 1000, the number of targets K = 5000 and the termination condition Θn = δ(n − 50 000) and are averaged over 100 realizations.
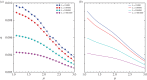
 versus the power-law exponent μ. (b) The total moving distance in exploration
versus the power-law exponent μ. (b) The total moving distance in exploration  versus μ. (c) The total moving distance in return
versus μ. (c) The total moving distance in return  versus μ. (d) The ratio of
versus μ. (d) The ratio of  to the total number of steps
to the total number of steps  versus μ. In panels (a–d), the dots represent simulations results and the dashed lines are a guide to the eye. Different colours correspond to different values of β, as indicated in the legend of panel (a). The results are obtained from numerical simulation with the landscape size L = 1000, the number of targets K = 5000 and the termination condition Θn = δ(n − 50 000) and are averaged over 100 realizations.
versus μ. In panels (a–d), the dots represent simulations results and the dashed lines are a guide to the eye. Different colours correspond to different values of β, as indicated in the legend of panel (a). The results are obtained from numerical simulation with the landscape size L = 1000, the number of targets K = 5000 and the termination condition Θn = δ(n − 50 000) and are averaged over 100 realizations.References
-
- Bartumeus F. 2007. Lévy processes in animal movement: an evolutionary hypothesis. Fractals 15, 151–162. (10.1142/S0218348X07003460) - DOI
-
- Ortiz-Pelaez A, Pfeiffer D, Soares-Magalhaes R, Guitian F. 2006. Use of social network analysis to characterize the pattern of animal movements in the initial phases of the 2001 foot and mouth disease (FMD) epidemic in the UK. Prev. Vet. Med. 76, 40–55. (10.1016/j.prevetmed.2006.04.007) - DOI - PubMed
-
- Bousquet F, Le Page C. 2004. Multi-agent simulations and ecosystem management: a review. Ecol. Model. 176, 313–332. (10.1016/j.ecolmodel.2004.01.011) - DOI
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials

