The point of no return: A fundamental limit on the ability to control thought and action
- PMID: 25633089
- PMCID: PMC4417067
- DOI: 10.1080/17470218.2015.1008020
The point of no return: A fundamental limit on the ability to control thought and action
Abstract
Bartlett (1958. Thinking. New York: Basic Books) described the point of no return as a point of irrevocable commitment to action, which was preceded by a period of gradually increasing commitment. As such, the point of no return reflects a fundamental limit on the ability to control thought and action. I review the literature on the point of no return, taking three perspectives. First, I consider the point of no return from the perspective of the controlled act, as a locus in the architecture and anatomy of the underlying processes. I review experiments from the stop-signal paradigm that suggest that the point of no return is located late in the response system. Then I consider the point of no return from the perspective of the act of control that tries to change the controlled act before it becomes irrevocable. From this perspective, the point of no return is a point in time that provides enough "lead time" for the act of control to take effect. I review experiments that measure the response time to the stop signal as the lead time required for response inhibition in the stop-signal paradigm. Finally, I consider the point of no return in hierarchically controlled tasks, in which there may be many points of no return at different levels of the hierarchy. I review experiments on skilled typing that suggest different points of no return for the commands that determine what is typed and the countermands that inhibit typing, with increasing commitment to action the lower the level in the hierarchy. I end by considering the point of no return in perception and thought as well as action.
Keywords: Cognitive control; Hierarchical control; Point of no return; Response inhibition; Stop signal.
Figures









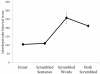
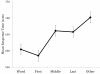


Similar articles
-
Fore-period effect and stop-signal reaction time.Exp Brain Res. 2005 Nov;167(2):305-9. doi: 10.1007/s00221-005-0110-2. Epub 2005 Nov 15. Exp Brain Res. 2005. PMID: 16160823
-
Mechanisms and dynamics of cortical motor inhibition in the stop-signal paradigm: a TMS study.J Cogn Neurosci. 2010 Feb;22(2):225-39. doi: 10.1162/jocn.2009.21248. J Cogn Neurosci. 2010. PMID: 19400674
-
On the ability to inhibit thought and action: general and special theories of an act of control.Psychol Rev. 2014 Jan;121(1):66-95. doi: 10.1037/a0035230. Psychol Rev. 2014. PMID: 24490789
-
Physiological evidence for response inhibition in choice reaction time tasks.Brain Cogn. 2004 Nov;56(2):153-64. doi: 10.1016/j.bandc.2004.06.004. Brain Cogn. 2004. PMID: 15518932 Review.
-
Proactive and reactive control of movement are differently affected in Attention Deficit Hyperactivity Disorder children.Res Dev Disabil. 2013 Oct;34(10):3104-11. doi: 10.1016/j.ridd.2013.06.032. Epub 2013 Jul 22. Res Dev Disabil. 2013. PMID: 23886755
Cited by
-
Effects of motor restrictions on preparatory brain activity.Exp Brain Res. 2021 Nov;239(11):3189-3203. doi: 10.1007/s00221-021-06190-w. Epub 2021 Aug 25. Exp Brain Res. 2021. PMID: 34432108 Free PMC article.
-
A sensorimotor control framework for understanding emotional communication and regulation.Neurosci Biobehav Rev. 2020 May;112:503-518. doi: 10.1016/j.neubiorev.2020.02.014. Epub 2020 Feb 15. Neurosci Biobehav Rev. 2020. PMID: 32070695 Free PMC article. Review.
-
Go-activation endures following the presentation of a stop-signal: evidence from startle.J Neurophysiol. 2017 Jan 1;117(1):403-411. doi: 10.1152/jn.00567.2016. Epub 2016 Nov 2. J Neurophysiol. 2017. PMID: 27832599 Free PMC article.
-
PROTOCOL: the On Track 2.0 cluster randomized teacher-led intervention to support executive function and self-regulation.Front Psychol. 2025 Jun 24;16:1574860. doi: 10.3389/fpsyg.2025.1574860. eCollection 2025. Front Psychol. 2025. PMID: 40631056 Free PMC article.
-
No effects of 1 Hz offline TMS on performance in the stop-signal game.Sci Rep. 2023 Jul 18;13(1):11565. doi: 10.1038/s41598-023-38841-z. Sci Rep. 2023. PMID: 37463991 Free PMC article.
References
-
- Allport DA. Selection for action: Some behavioural and neurophysiological considerations of attention and action. In: Heuer H, Sanders AF, editors. Perspectives on perception and action. Erlbaum; Hillsdale, NJ: 1987. pp. 395–419.
-
- Anderson JR. How can the human mind occur in the physical universe? Oxford University Press; Oxford: 2007.
-
- Anderson MC, Ochsner KN, Kuhl B, Cooper J, Robertson E, Gabrieli SW, Glover GH, Gabrieli JD. Neural systems underlying the suppression of unwanted memories. Science. 2004;303:232–235. - PubMed
-
- Arrington CM, Logan GD. The cost of a voluntary task switch. Psychological Science. 2004;15:610–615. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials

