When less is more: non-monotonic spike sequence processing in neurons

Abstract

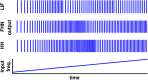
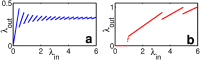
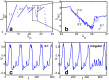
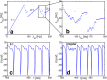
Fundamental response properties of neurons centrally underly the computational capabilities of both individual nerve cells and neural networks. Most studies on neuronal input-output relations have focused on continuous-time inputs such as constant or noisy sinusoidal currents. Yet, most neurons communicate via exchanging action potentials (spikes) at discrete times. Here, we systematically analyze the stationary spiking response to regular spiking inputs and reveal that it is generically non-monotonic. Our theoretical analysis shows that the underlying mechanism relies solely on a combination of the discrete nature of the communication by spikes, the capability of locking output to input spikes and limited resources required for spike processing. Numerical simulations of mathematically idealized and biophysically detailed models, as well as neurophysiological experiments confirm and illustrate our theoretical predictions.

Figure 1. Non-monotonic response to regular input spike sequences: increasing the input spike frequency may increase but also decrease the output spike frequency.

Bottom panel: input spike frequency that slowly increases ten-fold. Top three panels: output spike responses (LIF: leaky integrate-and-fire neuron with depressive synapse, FHN: Fitzhugh-Nagumo and HH: Hodgkin-Huxley neuron, both with static synapses). Time is rescaled so that all three data sets fit in this Figure. For details of models see equations (1)–(2) for LIF, equations (12)–(13) for FHN and equations (14)–(17) for HH.

Figure 2. Non-monotonic response functions of the idealized LIF synapse-neuron system.

Input-output response (a) for resource recovery that is much slower than the time scale of membrane potential leakage (τ = 1, μ = 10), for system with dynamics shown in Fig. 1, (b) for both processes occurring on the same time scales (τ = 1, μ = 1). In (a) only downward jumps, in (b) upward as well as downward jumps occur. Further parameters were u = 0.2, c = 0.5, V_eq = 0.8 for (a) and u = 0.4, c = 0.8, V_eq = 0 for (b).

Figure 3. Non-monotonic response in a Fitzhugh-Nagumo neuron receiving periodic input via a static synapse.

(a) Input-output response exhibits dominant n:1-locking interrupted by broad transition regions (b), magnified from (a). Several locking ratios n:m are indicated. In the transition regions, periodic, n:m-locked as well as nonperiodic, irregular dynamics arise. (c,d) Membrane potential dynamics (c) in the 4:1-locking region and (d) in the irregular regime. The model parameters were a = 0.139, b = 2.54, c = 0.5, μ′ = 125 and K(t) = 2(exp(−t)−exp(−2t)).

Figure 4. Non-monotonic response in a Hodgkin-Huxley neuron receiving periodic input via a static excitatory synapse.

(a) In the response curve n:1-locking regions are interrupted by broad transition regions (b), magnified from (a). In the transition regions nonperiodic, irregular dynamics arise. (c) and (d) show example dynamics of the membrane potential (c) in the 3:1-locking region (λ_in = 170Hz) and (d) in the irregular regime (λ_in = 140.2Hz). Simulation parameters were C = 2, V_Na = 50, V_K = −77, V_L = −54.4, g_Na = 120, g_K = 36, g_L = 0.3, I₀ = 5 and ε = 9. We used an alpha-function $K(t)=e\frac{t}{{\tau }_{\mathrm{\text{ex}}}}\exp (-t/{\tau }_{\mathrm{\text{ex}}})$ with time constant τ_ex = 1 to model the synaptic inputs (e is the Euler constant to normalize K(t)).

Figure 5. Non-monotonicity of response curves is robust against irregularity of the input.

Panels (a)–(c) show the input-output response of the LIF model system receiving input spike sequences with Gamma-distributed inter-spike intervals. The system parameters in (a) and (b) are identical to the system parameters in Fig. 2(a),(b). (c) shows the response of the system for parameters τ = 4, μ = 1, u = 0.2, c = 0.5 and V_eq = 0, where the inset demonstrates that for small input rates no output is generated. Inset of (b) shows the distribution for one fixed input rate, normalized to one. The shape parameter of the distribution was set to α = 100, so that the relative standard deviation of the input intervals is ${\sigma }_{\Delta t}/\overline{\Delta t}=0.1$.

Figure 6. Non-monotonic response to regular inputs as observed in MNTB-neurons from whole-cell patch-clamp recordings.

(a,b) Experimentally obtained response curves of two different MNTB-neurons for different pulse currents [(a) green: 375pA, orange, red: 425pA, blue: 450pA (b) orange: 575pA, red: 600pA, blue: 650pA]. The dashed lines indicate the major n:1-locking states predicted —no free fit parameter. Error bars indicate the estimated error made by calculating the mean output frequency from a finite number of output spikes. (c–f) Membrane potential dynamics for different locking types: (c) 1:1-locking, (d) 2:1-locking, (e) 3:1-locking, (f) unlocked, irregular dynamics. The letters in (b) indicate the data points where these dynamics were observed.