Numerical implementation of multiple peeling theory and its application to spider web anchorages

Abstract

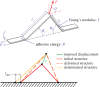
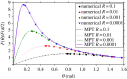
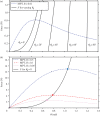
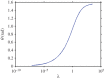
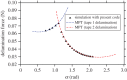
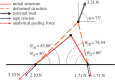
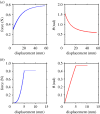
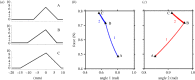
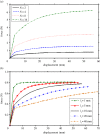
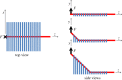
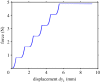
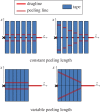
Adhesion of spider web anchorages has been studied in recent years, including the specific functionalities achieved through different architectures. To better understand the delamination mechanisms of these and other biological or artificial fibrillar adhesives, and how their adhesion can be optimized, we develop a novel numerical model to simulate the multiple peeling of structures with arbitrary branching and adhesion angles, including complex architectures. The numerical model is based on a recently developed multiple peeling theory, which extends the energy-based single peeling theory of Kendall, and can be applied to arbitrarily complex structures. In particular, we numerically show that a multiple peeling problem can be treated as the superposition of single peeling configurations even for complex structures. Finally, we apply the developed numerical approach to study spider web anchorages, showing how their function is achieved through optimal geometrical configurations.

Keywords: adhesion; multiple peeling; numerical simulations; spider web anchorages.

Figure 1.

(a) Schematic geometry of an asymmetrical double peeling configuration. (b) Comparison between initial, deformed and delaminated configurations. For simplicity, delamination is shown on only one of the two branches.

Figure 2.

Analytically (MPT) and numerically calculated results for normalized delamination load F(θ)/F(π/2) versus peeling angle θ in a symmetrical double peeling configuration for various adhesive energies R (in J mm⁻²).

Figure 3.

External applied force F and tape peeling forces versus peeling angle θ in symmetrical loading of a double peeling symmetric configuration: (a) R = 0.01, varying θ₀; (b) θ₀ = 0, varying R. The intersection between curves occurs for θ₀ = 0 at the maxima of the peeling force curves (indicated with crosses), i.e. for optimal peeling angle values.

Figure 4.

Optimal peeling angle θ = θ_opt as a function of the non-dimensional parameter λ

Figure 5.

Delamination force versus applied force for a double peeling case for a quasi-rigid tape (small λ), calculated numerically (triangles) and by MPT (lines).

Figure 6.

Graphical representation of system 1 in table 1, showing that numerically calculated peeling forces coincide with MPT-calculated ones where delamination occurs, if the deformed configuration is considered.

Figure 7.

Symmetrical double peeling simulations. (a) Delamination force and peeling angle as a function of the delamination length starting from θ = 90°. (b) Delamination force and peeling angle as a function of the displacement starting from θ = 0°.

Figure 8.

Delamination phases in a symmetrical double peeling simulation with a non-vertical force: (a) configuration at three successive time steps: A, B and C; (b) corresponding force versus peeling angle on the left tape; and (c) corresponding force versus peeling angle on the right tape. (Online version in colour.)

Figure 9.

Spider silk attachment structures: (a) schematic of a ‘staple-pin’ architecture, (b) detail of a fluid-coated silk fibre, (c) schematic of a ‘dendritic’ architecture, (d) optical micrograph of spider web generic anchorage (adapted from [22]; copyright © 2009, the American Society for Biochemistry and Molecular Biology) also showing details of the fluid-coated silk fibre (indicated by an arrow) and (e) optical micrograph of a staple-pin anchorage. (Online version in colour.)

Figure 10.

Force-diplacement curves for a dendritic anchorage, for (a) varying number N of fibres in the anchorage (l_i = 10 mm) and (b) varying detached length l_i of the anchorage (N = 2).

Figure 11.

Schematic of the delamination mechanism in a staple-pin anchorage. (Online version in colour.)

Figure 12.

Force–extension curves for a staple-pin anchorage. (Online version in colour.)

Figure 13.

Mechanism for increasing the peeling length (and force) in a staple-pin anchorage: the peeling line increases its angle with respect to z as the delamination proceeds along z. (Online version in colour.)