Quantum speed limits in open systems: non-Markovian dynamics without rotating-wave approximation
- PMID: 25676589
- PMCID: PMC4649631
- DOI: 10.1038/srep08444
Quantum speed limits in open systems: non-Markovian dynamics without rotating-wave approximation
Abstract
We derive an easily computable quantum speed limit (QSL) time bound for open systems whose initial states can be chosen as either pure or mixed states. Moreover, this QSL time is applicable to either Markovian or non-Markovian dynamics. By using of a hierarchy equation method, we numerically study the QSL time bound in a qubit system interacting with a single broadened cavity mode without rotating-wave, Born and Markovian approximation. By comparing with rotating-wave approximation (RWA) results, we show that the counter-rotating terms are helpful to increase evolution speed. The problem of non-Markovianity is also considered. We find that for non-RWA cases, increasing system-bath coupling can not always enhance the non-Markovianity, which is qualitatively different from the results with RWA. When considering the relation between QSL and non-Markovianity, we find that for small broadening widths of the cavity mode, non-Markovianity can increase the evolution speed in either RWA or non-RWA cases, while, for larger broadening widths, it is not true for non-RWA cases.
Figures
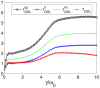
 are derived from the operator norm, trace norm and Hilbert-Schmidt norm in Ref. . The actual driving time τ = 30.
are derived from the operator norm, trace norm and Hilbert-Schmidt norm in Ref. . The actual driving time τ = 30.
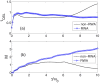

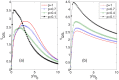
Similar articles
-
Relationship between quantum speed limit time and memory time in a photonic-band-gap environment.Sci Rep. 2016 Dec 23;6:39110. doi: 10.1038/srep39110. Sci Rep. 2016. PMID: 28008937 Free PMC article.
-
Minimal evolution time and quantum speed limit of non-Markovian open systems.Sci Rep. 2015 Nov 13;5:16357. doi: 10.1038/srep16357. Sci Rep. 2015. PMID: 26565062 Free PMC article.
-
Non-Markovianity of qubit evolution under the action of spin environment.Sci Rep. 2019 Feb 27;9(1):2987. doi: 10.1038/s41598-019-39140-2. Sci Rep. 2019. PMID: 30814544 Free PMC article.
-
Lindbladian approximation beyond ultraweak coupling.Phys Rev E. 2021 Jul;104(1-1):014110. doi: 10.1103/PhysRevE.104.014110. Phys Rev E. 2021. PMID: 34412241
-
Quantum Collision Models: A Beginner Guide.Entropy (Basel). 2022 Sep 7;24(9):1258. doi: 10.3390/e24091258. Entropy (Basel). 2022. PMID: 36141146 Free PMC article. Review.
Cited by
-
Quantum speed limit based on the bound of Bures angle.Sci Rep. 2020 Mar 26;10(1):5500. doi: 10.1038/s41598-020-62409-w. Sci Rep. 2020. PMID: 32218480 Free PMC article.
-
Relationship between quantum speed limit time and memory time in a photonic-band-gap environment.Sci Rep. 2016 Dec 23;6:39110. doi: 10.1038/srep39110. Sci Rep. 2016. PMID: 28008937 Free PMC article.
-
Quantum speed limit and a signal of quantum criticality.Sci Rep. 2016 Jan 19;6:19308. doi: 10.1038/srep19308. Sci Rep. 2016. PMID: 26782296 Free PMC article.
-
Control quantum evolution speed of a single dephasing qubit for arbitrary initial states via periodic dynamical decoupling pulses.Sci Rep. 2017 Mar 8;7:43654. doi: 10.1038/srep43654. Sci Rep. 2017. PMID: 28272546 Free PMC article.
-
Minimal evolution time and quantum speed limit of non-Markovian open systems.Sci Rep. 2015 Nov 13;5:16357. doi: 10.1038/srep16357. Sci Rep. 2015. PMID: 26565062 Free PMC article.
References
-
- Lloyd S. & Maccone L. Advances in quantum metrology. Nature Photonics 5, 222; 10.1038/nphoton.2011.35 (2011). - DOI
LinkOut - more resources
Full Text Sources
Other Literature Sources

