Simulating the entropic collapse of coarse-grained chromosomes

Abstract

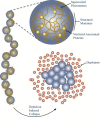
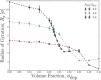
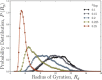
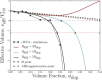
Depletion forces play a role in the compaction and decompaction of chromosomal material in simple cells, but it has remained debatable whether they are sufficient to account for chromosomal collapse. We present coarse-grained molecular dynamics simulations, which reveal that depletion-induced attraction is sufficient to cause the collapse of a flexible chain of large structural monomers immersed in a bath of smaller depletants. These simulations use an explicit coarse-grained computational model that treats both the supercoiled DNA structural monomers and the smaller protein crowding agents as combinatorial, truncated Lennard-Jones spheres. By presenting a simple theoretical model, we quantitatively cast the action of depletants on supercoiled bacterial DNA as an effective solvent quality. The rapid collapse of the simulated flexible chromosome at the predicted volume fraction of depletants is a continuous phase transition. Additional physical effects to such simple chromosome models, such as enthalpic interactions between structural monomers or chain rigidity, are required if the collapse is to be a first-order phase transition.

Figure 1

The coarse-grained model of bacterial chromosomal DNA after Jun and Wright (5). Structural monomers of supercoiled plectonemes of DNA are locally stabilized to form a cross-linked gel by various nucleoid-associated proteins. The chromosome is considered to be a linear chain of structural monomers. Surrounding proteins act as molecular crowding agents that can lead to collapse to a condensed state. To see this figure in color, go online

Figure 2

The radii of gyration of N_SM = 15 chains of combinatorial-WCA structural monomers as a function of depletant volume fraction, ϕ_dep. The observed transition to a collapsed state varies as a function of the size ratio R_SM/R_dep. To see this figure in color, go online.

Figure 3

Distributions of radii of gyration R_g for the size ratio of R_SM/R_dep = 5 and various volume fractions of depletants. The volume fractions shown are in the transition region near the critical volume fraction of depletants ${\varphi }_{\text{dep}}^{\ast }$, but the probability distributions remain unimodal. There appears to be no coexistence of both swollen and collapsed coils. To see this figure in color, go online.

Figure 4

The effective volume of structural monomers interacting via depletant-induced pair potentials as a function of depletant volume fraction ϕ_dep. Simulation results for the size ratio of R_SM/R_dep = 5 (black squares) compare well with both the linear AO (dashed lines) and the MT (solid lines) models at low volume fractions, approaching the physical volume $V_{\text{SM}}^{\prime }$ as ϕ_dep → 0. At higher volume fractions the simulations and MT model drop rapidly to negative values, passing through the θ-point ${\nu }_{\text{eff}}^{\Theta }$ (blue dotted line and circles) and the AHS-agglomeration point ${\nu }_{\text{eff}}^{{\ast }_{\text{AHS}}}$ (red dash-dot line and triangles). To see this figure in color, go online.

Figure 5

The order parameter Φ ≡ (R_g – R_glob)/(R_athermal – R_glob) reduces the radius of gyration axis of Fig. 2. When plotted against the rescaled volume fraction ${\varphi }_{\text{dep}}/{\varphi }_{\text{dep}}^{{\ast }_{\text{cWCA}}}$, the simulation curves for R_SM/R_dep = {3, 4, 5} collapse to a single curve. The theory results from substituting the effective volume from Eq. 10 into the Flory theory (Eq. 4) and estimating the AHS-agglomeration point ${\varphi }_{\text{dep}}^{{\ast }_{\text{AHS}}}$ as the critical volume fraction. (Dashed curve) In addition to the size ratios simulated, the Flory prediction for a larger size ratio of R_SM/R_dep = 20 is also indicated. To see this figure in color, go online.