Context-dependent memory decay is evidence of effort minimization in motor learning: a computational study

Abstract

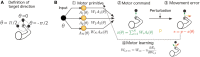
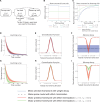
Recent theoretical models suggest that motor learning includes at least two processes: error minimization and memory decay. While learning a novel movement, a motor memory of the movement is gradually formed to minimize the movement error between the desired and actual movements in each training trial, but the memory is slightly forgotten in each trial. The learning effects of error minimization trained with a certain movement are partially available in other non-trained movements, and this transfer of the learning effect can be reproduced by certain theoretical frameworks. Although most theoretical frameworks have assumed that a motor memory trained with a certain movement decays at the same speed during performing the trained movement as non-trained movements, a recent study reported that the motor memory decays faster during performing the trained movement than non-trained movements, i.e., the decay rate of motor memory is movement or context dependent. Although motor learning has been successfully modeled based on an optimization framework, e.g., movement error minimization, the type of optimization that can lead to context-dependent memory decay is unclear. Thus, context-dependent memory decay raises the question of what is optimized in motor learning. To reproduce context-dependent memory decay, I extend a motor primitive framework. Specifically, I introduce motor effort optimization into the framework because some previous studies have reported the existence of effort optimization in motor learning processes and no conventional motor primitive model has yet considered the optimization. Here, I analytically and numerically revealed that context-dependent decay is a result of motor effort optimization. My analyses suggest that context-dependent decay is not merely memory decay but is evidence of motor effort optimization in motor learning.

Keywords: context-dependent memory decay; effort minimization; motor learning; motor primitive; neural network modeling.

Figure 1

Schematic diagram of the computational model and assumed task. (A) Definition of the target direction. θ = 0 is defined as the target for the straight-forward reaching movement. (B) The target direction (desired movement direction) θ_t determined the activities of the motor primitives A_i(θ_t) in the t-th trial. The task was to generate a motor command x_t to compensate for an environmental change (perturbation) p_t. The motor command x_t was determined by a linear combination of motor primitive activities, ${\displaystyle {\sum }_{i=1}^N{W}_i{A}_i({\theta }_t)}$, and these linear coefficients were modified to minimize a cost function E_t (e.g., the squared movement error and effort): $W_{i,t+1}=W_{i,t}-\eta \frac{\partial E_t}{\partial W_{i,t}}$. These procedures are summarized in the Summary of the Motor Primitive Framework Section in the Materials and Methods.

Figure 2

Results of simulation 1. (A) Simulated experimental setting in simulation 1. This setting consisted of 100 training trials, 100 test trials, and 50 retest trials. In the training trials, the (simulated) subjects were required to adapt to p = π/4 during reaching movements toward θ = 0. In the test trials, “error clamp” trials in which the movement error e was forcibly set to 0 were imposed. In these trials, θ = 0 (blue line in B–F), θ = π/12 (green line in B–F), θ = π/6 (red line in B–F), and θ = π/4 (cyan line in B–F). After these test trials, another 50 error clamp trials were imposed with θ = 0. The vertical black dotted lines denote the trials in which the training trials were switched to the test trials and the test trials were switched to the retest trials. (B) Trial-by-trial variation in the motor command x in the motor primitive framework with a weight decay. (C) Trial-by-trial variation in the motor command in the state space model with effort minimization. (D) Trial-by-trial variation in the motor command in the motor primitive framework with effort minimization. (E,F) Trial-by-trial variation in the motor command in the motor primitive framework with effort minimization when p = π/6 in (E) and p = π/12 in (F).

Figure 3

Results of simulation 2. (A) Simulated experimental setting for simulation 2. Training trials were conducted for 200 trials with θ = 0. After the training, 20 test trials with ${\theta }^{\prime }=-\pi +2\pi \frac{k}{K}$ and 100 relearning trials with θ = 0 were alternately simulated for K cycles, where K = 16, and the integer k was pseudorandomly sampled from the range [0, K − 1] to assume different values in each cycle. In the test trials, the movement error was forcibly set to 0 assuming error clamp trials. (B) Trial-by-trial variation of the motor command x in the test trials with the motor primitive framework with effort minimization, θ′ = 0 (blue line), θ′ = π/12 (green line), θ′ = π/6 (red line), and θ′ = π/3 (cyan line). The vertical black dotted line indicates the 10th test trial. (C) Trial-by-trial variation of the motor command in the relearning trials with the motor primitive framework with effort minimization. The black dotted line denotes the trial-by-trial variation of the motor command in the relearning trials with the motor primitive framework with weight decay (independent of θ′). The vertical black dotted line indicates the 10th relearning trial. (D) Learning curves. The horizontal axis indicates the trial number, and the vertical axis denotes the movement error e_t. The red line, blue line, and circle denote the trial-by-trial variation of e_t averaged across 20 simulation runs in the motor primitive framework with effort minimization, the framework with weight decay, and the state space model with effort minimization, respectively. The red and blue shaded areas indicate the standard deviations of the learning curves in the 20 simulation runs in the motor primitive framework with effort minimization and those with weight decay, respectively. After 200 trials, the motor commands x₂₀₀(0) converged to x₀ in all three models. (E) Generalization function averaged across 20 simulation runs. The horizontal axis indicates the tested movement direction θ′, and the vertical axis indicates the motor command x(θ′). To draw the generalization function, I averaged the motor commands of the initial 10 test trials in each cycle (the 10th test trial is indicated by the vertical black dotted line in B). The red and blue shaded areas indicate the standard deviation of the generalization function in the 20 simulation runs in the motor primitive frameworks with effort minimization and weight decay, respectively. (F) Context-dependent decay investigated in the relearning phase with θ′ = 0. The horizontal axis indicates the tested movement direction θ′, and the vertical axis indicates the normalized motor command in relearning trials. The normalized motor command was defined as $\frac{1}{10}{\displaystyle {\sum }_{t=1}^{10}{x}_{\text{relearning},\text{t}}(0)/x_0}$, where x_{relearning, t}(0) is a motor command at the t-th relearning trial in each cycle, i.e., I averaged the motor commands of the initial 10 relearning trials in each cycle (the 10th relearning trial is indicated by the vertical black dotted line in C) and divided the averaged value by x₀. The red and blue shaded areas indicate the standard deviations of the memory decays in the 20 simulation runs in the motor primitive frameworks with effort minimization and weight decay, respectively. (D,E,F) Parameter sensitivities of the learning curve, the generalization function, and the context-dependent memory decay in the motor primitive with effort minimization. The red lines denote the generalization function and the context-dependent decay with η = 0.5 and λ = 0.03, and the green lines denote those with η = 0.8 and λ = 0.01. The red and green shaded areas indicate the standard deviations of the learning curves in the 20 simulation runs in the motor primitive frameworks with effort minimization when η = 0.5 and λ = 0.03 and η = 0.8 and λ = 0.01, respectively.