A novel cortical thickness estimation method based on volumetric Laplace-Beltrami operator and heat kernel
- PMID: 25700360
- PMCID: PMC4405465
- DOI: 10.1016/j.media.2015.01.005
A novel cortical thickness estimation method based on volumetric Laplace-Beltrami operator and heat kernel
Abstract
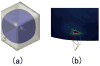
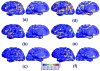
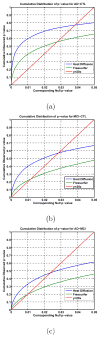
Cortical thickness estimation in magnetic resonance imaging (MRI) is an important technique for research on brain development and neurodegenerative diseases. This paper presents a heat kernel based cortical thickness estimation algorithm, which is driven by the graph spectrum and the heat kernel theory, to capture the gray matter geometry information from the in vivo brain magnetic resonance (MR) images. First, we construct a tetrahedral mesh that matches the MR images and reflects the inherent geometric characteristics. Second, the harmonic field is computed by the volumetric Laplace-Beltrami operator and the direction of the steamline is obtained by tracing the maximum heat transfer probability based on the heat kernel diffusion. Thereby we can calculate the cortical thickness information between the point on the pial and white matter surfaces. The new method relies on intrinsic brain geometry structure and the computation is robust and accurate. To validate our algorithm, we apply it to study the thickness differences associated with Alzheimer's disease (AD) and mild cognitive impairment (MCI) on the Alzheimer's Disease Neuroimaging Initiative (ADNI) dataset. Our preliminary experimental results on 151 subjects (51 AD, 45 MCI, 55 controls) show that the new algorithm may successfully detect statistically significant difference among patients of AD, MCI and healthy control subjects. Our computational framework is efficient and very general. It has the potential to be used for thickness estimation on any biological structures with clearly defined inner and outer surfaces.
Keywords: Cortical thickness; False discovery rate; Heat kernel; Spectral analysis; Tetrahedral mesh.
Copyright © 2015 Elsevier B.V. All rights reserved.
Figures
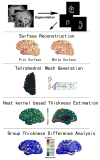


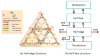
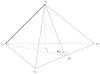
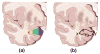







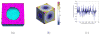
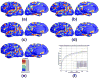
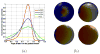
Similar articles
-
Towards a Holistic Cortical Thickness Descriptor: Heat Kernel-Based Grey Matter Morphology Signatures.Neuroimage. 2017 Feb 15;147:360-380. doi: 10.1016/j.neuroimage.2016.12.014. Epub 2016 Dec 26. Neuroimage. 2017. PMID: 28033566 Free PMC article.
-
Individual subject classification for Alzheimer's disease based on incremental learning using a spatial frequency representation of cortical thickness data.Neuroimage. 2012 Feb 1;59(3):2217-30. doi: 10.1016/j.neuroimage.2011.09.085. Epub 2011 Oct 8. Neuroimage. 2012. PMID: 22008371 Free PMC article.
-
Multi-scale Heat Kernel based Volumetric Morphology Signature.Med Image Comput Comput Assist Interv. 2015;9351:751-9. doi: 10.1007/978-3-319-24574-4_90. Med Image Comput Comput Assist Interv. 2015. PMID: 26550613 Free PMC article.
-
Sulcal morphology changes and their relationship with cortical thickness and gyral white matter volume in mild cognitive impairment and Alzheimer's disease.Neuroimage. 2008 Oct 15;43(1):103-13. doi: 10.1016/j.neuroimage.2008.07.016. Epub 2008 Jul 22. Neuroimage. 2008. PMID: 18691657
-
Structural magnetic resonance imaging for the early diagnosis of dementia due to Alzheimer's disease in people with mild cognitive impairment.Cochrane Database Syst Rev. 2020 Mar 2;3(3):CD009628. doi: 10.1002/14651858.CD009628.pub2. Cochrane Database Syst Rev. 2020. PMID: 32119112 Free PMC article.
Cited by
-
Tetrahedral spectral feature-Based bayesian manifold learning for grey matter morphometry: Findings from the Alzheimer's disease neuroimaging initiative.Med Image Anal. 2021 Aug;72:102123. doi: 10.1016/j.media.2021.102123. Epub 2021 Jun 8. Med Image Anal. 2021. PMID: 34214958 Free PMC article.
-
Towards a Holistic Cortical Thickness Descriptor: Heat Kernel-Based Grey Matter Morphology Signatures.Neuroimage. 2017 Feb 15;147:360-380. doi: 10.1016/j.neuroimage.2016.12.014. Epub 2016 Dec 26. Neuroimage. 2017. PMID: 28033566 Free PMC article.
-
Recent publications from the Alzheimer's Disease Neuroimaging Initiative: Reviewing progress toward improved AD clinical trials.Alzheimers Dement. 2017 Apr;13(4):e1-e85. doi: 10.1016/j.jalz.2016.11.007. Epub 2017 Mar 22. Alzheimers Dement. 2017. PMID: 28342697 Free PMC article. Review.
-
Studying ventricular abnormalities in mild cognitive impairment with hyperbolic Ricci flow and tensor-based morphometry.Neuroimage. 2015 Jan 1;104:1-20. doi: 10.1016/j.neuroimage.2014.09.062. Epub 2014 Oct 5. Neuroimage. 2015. PMID: 25285374 Free PMC article.
-
Isometry Invariant Shape Descriptors for Abnormality Detection on Brain Surfaces Affected by Alzheimer's Disease.Annu Int Conf IEEE Eng Med Biol Soc. 2018 Jul;2018:427-4631. doi: 10.1109/EMBC.2018.8513129. Annu Int Conf IEEE Eng Med Biol Soc. 2018. PMID: 30440425 Free PMC article.
References
-
- Alzheimer’s Association. Alzheimer’s disease facts and figures. Alzheimer’s Association; 2012. http://www.alz.org. - PubMed
-
- Benjamini Y, Hochberg Y. Controlling the False Discovery Rate: A Practical and Powerful Approach to Multiple Testing. Journal of the Royal Statistical Society Series B (Methodological) 1995;57:289–300.
-
- Berg L. Clinical Dementia Rating (CDR) Psychopharmacol Bull. 1988;24:637–639. - PubMed
-
- Braak H, Braak E. Neuropathological stageing of Alzheimer-related changes. Acta Neuropathol. 1991;82:239–259. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

