Critical slowing down governs the transition to neuron spiking

Abstract

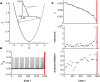
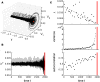
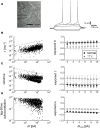
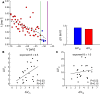
Many complex systems have been found to exhibit critical transitions, or so-called tipping points, which are sudden changes to a qualitatively different system state. These changes can profoundly impact the functioning of a system ranging from controlled state switching to a catastrophic break-down; signals that predict critical transitions are therefore highly desirable. To this end, research efforts have focused on utilizing qualitative changes in markers related to a system's tendency to recover more slowly from a perturbation the closer it gets to the transition--a phenomenon called critical slowing down. The recently studied scaling of critical slowing down offers a refined path to understand critical transitions: to identify the transition mechanism and improve transition prediction using scaling laws. Here, we outline and apply this strategy for the first time in a real-world system by studying the transition to spiking in neurons of the mammalian cortex. The dynamical system approach has identified two robust mechanisms for the transition from subthreshold activity to spiking, saddle-node and Hopf bifurcation. Although theory provides precise predictions on signatures of critical slowing down near the bifurcation to spiking, quantitative experimental evidence has been lacking. Using whole-cell patch-clamp recordings from pyramidal neurons and fast-spiking interneurons, we show that 1) the transition to spiking dynamically corresponds to a critical transition exhibiting slowing down, 2) the scaling laws suggest a saddle-node bifurcation governing slowing down, and 3) these precise scaling laws can be used to predict the bifurcation point from a limited window of observation. To our knowledge this is the first report of scaling laws of critical slowing down in an experiment. They present a missing link for a broad class of neuroscience modeling and suggest improved estimation of tipping points by incorporating scaling laws of critical slowing down as a strategy applicable to other complex systems.

Fig 1. Critical slowing down before neuronal spiking in a pyramidal neuron.

a, Current stimulation protocol, gray areas mark segments from which variance and autocorrelation were calculated, black areas segments used to determine recovery rates. b, Time course of the membrane potential subject to brief perturbations by current injections on top of a slowly depolarizing step current. The inset shows a magnification of the voltage response to a short current injection and an exponential fit to its recovery (red line). c, Recovery rates λ after perturbations, variance and lag-50ms autocorrelation in the subthreshold voltage, in this case for a pyramidal neuron.

Fig 2. Illustration of stochastic scaling laws near the saddle-node (fold) bifurcation in a model system.

a, Phase space with a single stochastic sample path (black) of a saddle-node bifurcation (eq. 10) for the initial condition (V(0), y(0)) = (−4, 1.6) with σ ₁ = 0.001, ϵ = 0.001 and small perturbations of size σ ₂(t _i) = 0.1 with t _i = 60. The bifurcation occurs at (V _c, y _c) = (0, 0) (red dot). The gray curves are the system equilibria (for ϵ = 0). b, Sample path V _d plotted as a time series where the equilibrium values have been subtracted (i.e. detrending along the equilibrium branch). c, Scaling of recovery rate λ, variance v and autocorrelation as dynamics approaches the bifurcation point (red vertical line). Recovery rate and variance follow a power-law scaling with exponents ±0.5 illustrated by black dashed lines.

Fig 3. Illustration of stochastic scaling laws near the subcritical Hopf bifurcation in a model system.

a, Phase space with a single stochastic sample path (black) of a Hopf bifurcation (eq. 12) for the initial condition (V ₁(0), V ₂(0), y ₀) = (0, 0, −2) with σ _{1, 2} = 0.001, ϵ = 0.001 and small perturbations of size σ ₃(t _i) = 0.005 with t _i = 60. The bifurcation occurs at (V _1c, V _2c, y _c) = (0, 0, 0) (red dot). b, Sample path V ₁ plotted as a time series used for further analysis. c, Scaling of recovery rate λ, variance v and autocorrelation as dynamics approaches the bifurcation point (red vertical line). Recovery rate and variance follow a power-law scaling with exponents ±1 illustrated by black dashed lines.

Fig 4. Scaling analysis of indicators related to critical slowing down in pyramidal neurons.

a, photomicrograph of a neuron with pyramidal morphology and typical responses to depolarizing and hyperpolarizing currents. b, Recovery rate as a function of ΔI, the distance to the bifurcation point, for all trials combined and fitted exponents averaged over individual trials and for different minimal values ΔI _min for normal conditions (right, black markers, standard deviation) and after bath application of tetrodotoxin (right, gray markers, standard deviation). c, Variance. d, Autocorrelation. Grey dashed lines on the left side show power-laws with exponent 0.5 for recovery rate, -0.5 for variance and -0.27 for autocorrelation.

Fig 5. Scaling analysis of indicators related to critical slowing down in fast-spiking (FS) neurons.

a, Photomicrograph of a typical FS neuron with round morphology and responses to depolarizing and hyperpolarizing currents. Right: the f-I relationship shows a discontinuity in frequency at the onset of spiking. Different markers correspond to different neurons; for comparability the injected current has been normalized to the onset of spiking. b, FS neurons (red markers) could be distinguished from pyramidal neurons (blue markers) by shorter spike width and greater afterhyperpolarization (AHP) values. c, Exponents (mean ± standard deviation) for recovery rate (θ, round markers) and variance (τ, diamonds) for different minimal values ΔI _min of the fit.

Fig 6. Prediction of the spiking threshold using scaling relations of critical slowing down.

a, The critical voltage V _c in pyramidal neurons was determined as a fit parameter by fitting recovery rates λ (red markers) excluding the last five measurements (blue markers) to voltage by λ = a(V _c−V)^θ. ΔV _p is the difference between the fitted critical voltage (red line) and the last value included in the fit (green line); ΔV _m, respectively, refers to the difference between the measured voltage at the onset of spiking (blue line) and the last value used in the fit (green line). b, Predicted ΔV _p and measured ΔV _m exhibit a significant correlation when fitted with exponent θ = 0.5 but not when fitted with exponent θ = 1.0 (c). P and R values refer to the linear regression analysis (solid black lines).