Visualizing transient dark states by NMR spectroscopy

Abstract

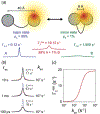
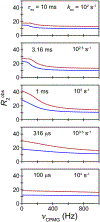
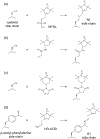
Myriad biological processes proceed through states that defy characterization by conventional atomic-resolution structural biological methods. The invisibility of these 'dark' states can arise from their transient nature, low equilibrium population, large molecular weight, and/or heterogeneity. Although they are invisible, these dark states underlie a range of processes, acting as encounter complexes between proteins and as intermediates in protein folding and aggregation. New methods have made these states accessible to high-resolution analysis by nuclear magnetic resonance (NMR) spectroscopy, as long as the dark state is in dynamic equilibrium with an NMR-visible species. These methods - paramagnetic NMR, relaxation dispersion, saturation transfer, lifetime line broadening, and hydrogen exchange - allow the exploration of otherwise invisible states in exchange with a visible species over a range of timescales, each taking advantage of some unique property of the dark state to amplify its effect on a particular NMR observable. In this review, we introduce these methods and explore two specific techniques - paramagnetic relaxation enhancement and dark state exchange saturation transfer - in greater detail.

Fig. 1.

NMR methods for characterizing a ‘dark’ state in exchange with a visible species. Simulated NMR spectra are shown for a resonance in exchange between two states (A and B) over a range of timescales. Shown from top to bottom are exchange lifetimes τ_ex =1 μs, 10 μs, 100 μs, 1 ms, 10 ms, 100 ms, and 1 s (𝓀_ex = 10⁶–10⁰ s⁻¹). Spectra were simulated by solving the McConnell equations (Eqs. (16)–(20)) (McConnell, 1958) in MATLAB for a chemical shift difference between states of Δω/2π = 120 Hz (e.g. 2 ppm for ¹⁵N on a 600 MHz spectrometer). In this example, state A is the major state (p_A = 75%), and state B is the minor state (p_B = 25%). On the left, states A and B have identical intrinsic rates of transverse relaxation $\left(R_2^0=10\hspace{0.17em}{\text{s}}^{-1}\right)$. On the right, state B has an enhanced intrinsic relaxation rate $\left(R_{2,B}^0=100\hspace{0.17em}{\text{s}}^{-1}\right)$, which could be due to a paramagnetic center or a slow rate of tumbling. In practice, p_B could be much lower and $R_{2,B}^0$ much larger, although less extreme values are used here for illustrative purposes. In the slow exchange regime (bottom), states A and B give rise to two separate peaks, although in practice state B may be invisible due to a low signal/noise ratio. In the fast exchange regime, a single peak is observed with a population-averaged chemical shift and apparent R₂. In the intermediate exchange regime (middle), the peaks undergo extreme chemical shift broadening, and the apparent R₂ is greatly enhanced due to R_ex. Down the center of the figure, NMR methods for characterizing dark states are shown, with a rough range of timescales over which they can be applied. The three methods shown toward the right (PRE, lifetime line broadening (R_llb), and DEST) are used to visualize a dark state with a greatly enhanced R₂ compared with the major state. The other methods shown, toward the left, depend on either a difference in chemical shift between states A and B (rotating frame relaxation dispersion (R_1ρ), CPMG relaxation dispersion, and CEST) or a difference in rates of hydrogen exchange.

Fig. 2.

Characterizing a sparsely populated state by PRE. If a major state (A) is in exchange with a minor state (B), the effect of the minor state can be amplified by PRE if two points (corresponding to the paramagnetic center and observed nucleus) are in closer proximity in the minor state than in the major state. (a) In this example, the protein is in exchange between an extended state (A, r = 40 Å) and a compact state (B, r = 8 Å). If a nitroxide spin label is attached to one point, the PRE measured for a proton at the other point would be virtually zero in state A (Γ_2,A = 0·12 s⁻¹), but very large in state B (Γ_2,B = 1900 s⁻¹) causing broadening of the observed NMR signal. PRE values were calculated assuming a correlation time of τ_c = 10 ns (corresponding to a protein at room temperature with a molecular weight of ∼20 kDa). Spectra were calculated by solving the McConnell equations (Eqs. (16)–(20) and (57)) in MATLAB, assuming R_2,dia = 10 s⁻¹ in each state (the height of the spectrum for state B [green] has been magnified 10⁷ times for the purposes of visualization). If states A and B are in fast exchange on the PRE timescale (in this example: 𝓀_ex ≫ Γ_2,A - Γ_2,B = 1900 s⁻¹; τ_ex ≪ 500 μs), the apparent PRE will be the population-averaged PRE of the two states $\left({\Gamma }_2^{\text{app}}=0.99\times 0.12\hspace{0.17em}{\text{s}}^{-1}+0.01\times 1900\hspace{0.17em}{\text{s}}^{-1}=19.12\hspace{0.17em}{\text{s}}^{-1}\right)$ Thus, even although state B comprises only 1% of the total population, ${\Gamma }_2^{\text{app}}$ arises almost exclusively from this minor state. (b) If the exchange rate is slower, the apparent PRE measured for A will be less than the population-weighted averaged PRE. Shown in black are simulated spectra for the system undergoing exchange with a rate of 𝓀_ex = 10², 10³, or 10⁴ s⁻¹. The dashed blue spectrum corresponds to the paramagnetic spectrum of A alone, and the dashed red spectrum corresponds to the population-weighted averaged paramagnetic spectrum under very fast exchange conditions (10⁶ s⁻¹). (c) Apparent PRE plotted against 𝓀_ex. The PRE increases from 0·12 s⁻¹ for a system undergoing very slow exchange (the value for state A alone) to 19·12 s⁻¹ for a system undergoing very fast exchange.

Fig. 3.

Characterizing exchange with a ‘dark’ state by CPMG relaxation dispersion. Relaxation dispersion curves were simulated in MATLAB, showing the apparent observed transverse relaxation rate $\left(R_2^{\text{obs}}\right)$ as a function of the repetition rate of 180° CPMG pulses (ν_CPMG, 0–1 kHz). Curves were calculated by solving the McConnell equations in MATLAB using Eq. (31). Curves are shown for range of exchange rates (𝓀_ex = 10²–10⁴ s⁻¹) for a system where a visible species (p_A = 95%) is in exchange with a dark state (p_B = 5%), analogous to a ¹⁵N resonance with a chemical shift difference between states A and B of Δδ = 2 ppm. The blue curves correspond to a static B₀ field strength of 600 MHz (Δω/2π = 120 Hz), and the red curves correspond to 900 MHz (Δω/2π = 180 Hz). At a large ν_CPMG, $R_2^{\text{obs}}$ approaches the intrinsic transverse relaxation rate $R_2^0$ (set here for both states to 10 s⁻¹ at 600 MHz and 13 s⁻¹ at 900 MHz). CPMG relaxation dispersion is most useful for characterizing exchange with a minor species when $R_{\text{ex}}\left(=R_2^{\text{obs}}\left[v_{\text{CPMG}}=0\right]-R_2^{\text{obs}}\left[v_{\text{CPMG}}\to \infty \right]\right)$ is largest, which occurs when 𝓀_ex = Δω (∼1000 s⁻¹, middle panel).

Fig. 4.

Characterizing ‘dark’ states by exchange saturation transfer. Saturation profiles are plotted for (a) CEST and (b) DEST experiments by solving the homogeneous McConnell equations (Eqs. (82)–(84)) in MATLAB. The y-axis gives the ratio of the peak intensity measured in the presence of a CW RF B₁ field (I_sat) over the peak intensity measured for a reference experiment in the absence of the saturation field (I_ref). The x-axis gives the frequency offset of the applied B₁ field. Note that the units are (a) in Hz for the CEST profiles, but are (b) in kHz for the DEST profiles, where the x-axis has been expanded almost 50 fold to accommodate the broader DEST profiles. B₁ field strengths (applied in the x-dimension) are (a) 2·5 Hz (green), 5 Hz (cyan), 10 Hz (blue), and 25 Hz (purple) for CEST and (b) 25 Hz (green), 50 Hz (cyan), 100 Hz (blue), and 250 kHz (purple) for DEST (i.e. the DEST experiment is performed at about one order of magnitude higher B₁ field strength than CEST). In this figure, a major visible state A (p_A = 95%) is separated from a minor dark state B (p_B = 5%) by a chemical shift difference of Δω/2π = 120 Hz (e.g. 2 ppm for ¹⁵N in a 600 MHz spectrometer). For the CEST profiles (a), $R_2^0=10\hspace{0.17em}{\text{s}}^{-1}$ and R₁ =1 s⁻¹ for both states. For the DEST profiles (b), $R_{2,B}^0=10\hspace{0.17em}000\hspace{0.17em}{\text{s}}^{-1}$. CW saturation was applied for 1 s (= 1 × T₁). Results are shown for a system undergoing no exchange (top; i.e. the saturation profile of the major visible species A alone), and exchange at a rate of 𝓀_ex = 1, 10, and 100 s⁻¹ (bottom). Full saturation of the signal (I_sat/I_ref = 0) occurs when the B₁ field is applied on resonance to state A, and saturation can be transferred from states B to A by exchange either from (a) on-resonance saturation of state B due to a different chemical shift (CEST) or (b) off-resonance saturation of the broader profile of state B due to its faster rate of transverse relaxation (DEST).

Fig. 5.

Enhanced apparent observed transverse relaxation rate $\left(R_2^{\text{obs}}\right)$ due to exchange with a minor species. Lifetime line broadening (R_llb, red), chemical shift exchange broadening (R_ex, green), their sum (R_llb + R_ex, blue), and the observed enhancement in apparent transverse relaxation rate ($\Delta R_2^{\text{obs}}$, black) compared with a system in the absence of exchange are plotted versus exchange rate. Curves are shown for a small, rapidly tumbling visible species (p_A = 95%, R⁰ = 10 s⁻¹) in exchange with a sparsely populated ‘dark’ state (p_B = 5%). On the left, simulated data are plotted using a linear scale for the y-axis (note that the scale varies between plots); on the right, a logarithmic scale is used for the y-axis (same scale in all plots); the x-axis is plotted with a logarithmic scale in all instances. The x-axis on the top of the plot shows the apparent first-order rate constant $\left({𝓀}_{\text{on}}^{\text{app}}\hspace{0.17em}\text{or}\hspace{0.17em}{𝓀}_{AB}\right)$ for molecules of state A going to state B. The x-axis on the bottom of the plot shows the overall exchange rate $\left({𝓀}_{\text{ex}}={𝓀}_{\text{on}}^{\text{app}}+{𝓀}_{\text{off}}={𝓀}_{\text{AB}}+{𝓀}_{\text{BA}}\right)$ (a) In the absence of a difference in $R_2^0$ between the two states, only R_ex is observed for a system with a difference in chemical shifts between the two states, which has a maximum value when 𝓀_ex = Δω. Here, Δω/2π = 120 Hz (e.g. 2 ppm for ¹⁵N in a 600 MHz static field). (b–d) If the two states differ in chemical shift and state B exhibits a faster transverse relaxation time – i.e. for a high-molecular-weight, slowly tumbling dark state – then $\Delta R_2^{\text{obs}}$ will have contributions from both R_ex and R_llb. In the slow exchange regime $\left({𝓀}_{\text{ex}}\gg R_{2,B}-R_{2,A}\hspace{0.17em}\text{and}\hspace{0.17em}{𝓀}_{\text{ex}}\ll \Delta \omega \right),\Delta R_2^{\text{obs}}=R_{\text{ex}}=R_{\text{llb}}={𝓀}_{\text{on}}^{\text{app}}$. In the fast exchange regime $\left({𝓀}_{\text{ex}}\gg R_{2,B}-R_{2,A}\hspace{0.17em}\text{and}\hspace{0.17em}{𝓀}_{\text{ex}}\gg \Delta \omega \right),\Delta R_2^{\text{obs}}=R_{\text{ex}}+R_{\text{llb}}$, and under very fast exchange, the value of R_ex approaches zero, and R_llb approaches a population-weighted maximum value (e.g. in panel (d), $\Delta R_2^{\text{max}}=500\hspace{0.17em}{\text{s}}^{-1}=5\%\times 10\hspace{0.17em}000\hspace{0.17em}{\text{s}}^{-1}$ ). Note that the same curve for R is shown in panels (a–d). (e) In the absence of a difference in chemical shift between the two states, only R_llb is observed for a system with a difference in $R_2^0$ between the two states. For all panels, $R_2^{\text{obs}}$ was determined by first solving the McConnell equations to generate a magnetization time course, which was then fit to the free induction decay of a single resonance with $R_2^{\text{obs}}$. A similar procedure was carried out to determine $R_2^{\text{obs}}$ in the absence of R_{llb $\left(R_2^{\text{obs}}\left[R_{2,B}=R_{2,A}\right]\right)$} and in the absence of Rex $\left(R_2^{\text{obs}}\left[\Delta \omega =0\right]\right)$ Values were calculated as follows for each exchange rate: $\Delta R_2^{\text{obs}}=R_2^{\text{obs}}-R_{2,A},\hspace{0.17em}{R}_{\text{llb}}=R_2^{\text{obs}}\left[\Delta \omega =0\right]-R_{2,A}$ and $R_{\text{ex}}=R_2^{\text{obs}}\left[R_{2,B}=R_{2,A}\right]-R_{2,A}$ All calculations were performed in MATLAB.

Fig. 6.

Site-directed spin labeling. Shown are four different chemistries for conjugating a spin label to a cysteine residue (a–c) or to an unnatural amino acid (d). All four examples are nitroxide spin labels (with the unpaired electron denoted with a dot), but the same chemistry can be used for spin labels that chelate a paramagnetic metal ion. The C_α of the peptide backbone is labeled. (a) Reaction of a methanethiosulfonate with cysteine to form a disulfide bond. The compound (1-oxyl-2,2,5,5-tetramethyl-Δ3-pyrroline-3-methyl) methanethiosulfonate (MTSL; left) reacts with cysteine to form the R1 side chain (right) (Battiste & Wagner, 2000; Gaponenko et al. 2000). (b) Reaction of an iodoacetamide with cysteine to form an S–C bond. Shown on the left is 3-(2-iodoacetamido)-2,2,5,5-tetramethyl-1-pyrolidinyloxy (iodoacetamido-PROXYL) (Gillespie & Shortle, 1997a). (c) Reaction of a maleimide with cysteine to form an S–C bond. Shown on the left is N-(1-oxyl-2,2,6,6-tetramethyl-4-piperidinyl) maleimide (maleimide-TEMPO) (Griffith & McConnell, 1966; Tang et al. 2008a). (d) Reaction of 3-aminooxymethyl-2,2,5,5-tetramethyl-2,5-dihydro-1H-pyrrol-1-yloxyl radical (HO-4120) with the unnatural amino acid p-acetyl-_L-phenylalanine to form the side chain K1 (Fleissner et al. 2009).

Fig. 7.

Spin label side chains for measuring PRE. Shown are three nitroxide spin label side chains (a, c, d), a diamagnetic control (b), and two side chains for chelating paramagnetic metal ions (e, f). The unpaired electron in each nitroxide side is denoted with a dot, and metal chelating sites are denoted with stars. The C_α of the peptide backbone is labeled. (a) The side chain R1, introduced by the reaction of (1-oxyl-2,2,5,5-tetramethyl-Δ3-pyrroline-3-methyl) methanethiosulfonate (MTSL) with a cysteine side chain (Battiste & Wagner, 2000; Gaponenko et al. 2000). (b) An acylated derivative of R1, which can be used as a diamagnetic control for R1/MTSL PRE studies, introduced by the reaction of (1-acetoxy-2,2,5,5-tetramethyl-δ−3-pyrroline-3-methyl) methanethiosulfonate with a cysteine side chain (Altenbach et al. 2001). (c) The side-chain R1p, a derivative of R1 that adopts a narrower range of conformations and simplifies analysis, introduced by the reaction of 3-methanesulfonilthiomethyl-4-(pyridin-3-yl)-2,2,5,5-tetramethyl-2,5-dihydro-1H-pyrrol-1-yloxyl radical (HO-3606) with a cysteine side chain (Fawzi et al. 2011a). (d) The side chain RX, which also is more rigid than R1, introduced by the reaction of 3,4-bis-(methanethiosulfonylmethyl)-2,2,5,5-tetramethyl-2,5-dihydro-1H-pyrrol-1-yloxy radical (HO-1944) with two cysteine side chains located within close proximity (specifically at i and i +3 or i + 4 in a helix or at i and i + 2 in a β-strand) (Fleissner et al. 2011). (e) A side chain for chelating paramagnetic metal ions (e.g. Mn²⁺) or diamagnetic controls (e.g. Ca²⁺), introduced by the reaction of S-(2-pyridylthio) cysteaminyl-EDTA with a cysteine side chain (Dvoretsky et al. 2002; Ebright et al. 1992; Ermacora et al. 1992). (f) The CLaNP (caged lanthanide NMR probe) tags chelate lanthanide ions and offer a more rigid paramagnetic center, suitable for both PRE and PCS measurements. Shown here is the side chain introduced by conjugating 1,4,7,10-tetraazacyclododecane-1,7-[di-(N-oxido-pyridine-2-yl)methyl]-4,10-bis (2-(acetylamino)ethylmethanesulfonothioate) (CLaNP-5) to two cysteine side chains located in close proximity to one another (Keizers et al. 2007, 2008).

Fig. 8.

Pulse sequences for 2D ¹H_N–Γ₂ PRE experiments. (a) HSQC-based pulse sequence for measuring 1H_N–Γ₂. Full details are given in Iwahara et al. (Iwahara et al. 2007). The delay T is incremented to measure ¹H_N transverse relaxation. Two 180° ¹⁵N pulses are applied to eliminate longitudinal cross-correlated relaxation interference between the ¹⁵N–¹H dipolar interaction and ¹⁵N chemical shift anisotropy. Although ³J_HN−Hα is active for non-deuterated proteins during the period T, the resulting modulation is cancelled out when Γ₂ is measured by the two-time-point method, using an equal delay T in both the paramagnetic experiment and the diamagnetic control. Alternatively, ³J_{HN Hα} can be directly cancelled by replacing the 180° ¹H pulse separating the two halves of delay T (arrow) with an IBURP2 pulse that selectively excites only the amide region of the ¹H spectrum. (b) TROSY pulse sequence for measuring ¹H_N–Γ₂. Note that in this pulse sequence the delay T (located at the end of the pulse sequence) is incremented to measure the slower-relaxing TROSY component of the ¹H_N transverse relaxation rate (although ¹H_N–Γ₂ is the same as for R₂ measurements). For proteins that are not deuterated, ³J_{HN Hα} can be cancelled out either by employing the two-time-point method or by replacing the final 180° ¹H pulse and adjacent soft water fiip-back pulses separating the two halves of delay T (arrow) with an IBURP2 pulse that selectively excites only the amide region of the ¹H spectrum. Unless otherwise indicated, all pulses have phase x; ϕ₁ = y, -y, -x, x; ϕ_rec = y, -y, x, -x. Quadrature detection in the indirect ¹⁵N dimension is achieved using the Rance-Kay echo/anti-echo scheme (Kay et al. 1992) by inverting gradients G3 and G3 and using phase ϕ₁ = y, -y, x, -x for the second free induction decay (FID) of each quadrature pair.

Fig. 9.

Visualizing sparsely populated compact ‘dark’ states in Ca²⁺ activation of CaM. (a) Structures of CaM in various physiological states. Ca²⁺ ions are shown as red spheres, and spin-labeling sites S17C and A128C are indicated by yellow spheres. The flexible linker (residues 77–81) is shown in magenta. (b) Experimental PRE profiles for Ca²⁺-loaded CaM (with a spin label at S17C or A128C), in the presence or absence of peptide, are shown as circles (error bar, 1 s.d.). PREs too large (>80 s⁻¹) to be accurately measured are plotted at the top of the charts. PRE profiles back-calculated from the structures of CaM– 4Ca²⁺–peptide (red) and CaM–4Ca²⁺ (blue) are shown as solid lines. Only for the CaM–4Ca²⁺–peptide complex are the experimental interdomain PREs correctly predicted by the corresponding known X-ray structure. The bottom panel shows the resulting fits for a minor state population of 10% represented by an eight-member ensemble (magenta lines). (c) Dependence of the interdomain PRE Q-factor for S17C (blue) and A128C (green) as a function of minor state population for CaM–4Ca²⁺. (d) Modeling interdomain association in CaM–4Ca²⁺ (measured by PREs) as a local concentration effect. Empirical values of effective molarity (circles) were calculated from interdomain PRE data for CaM–4Ca²⁺ with different linker lengths (Anthis & Clore, 2013). These data were fit to an equation describing the theoretical values of the effective concentration of two points at the end of a random coil linker, where the interaction only occurs when the two points are separated by a defined distance. The best-fit line is shown in red (units of mM) and is a product of a pre-exponential factor (green) and exponential factor (blue). (e) The complex of CaM–4Ca²⁺ with an MLCK peptide is shown with CaM in cyan and the peptide in blue overlaid on the CaM–4Ca²⁺ dumbbell structure (green), best-fitted to either the N-terminal (left panel) or C-terminal (right panel) domains. The gray probability density maps represent 26 additional peptide-bound structures overlaid in the same manner. (f) Atomic probability density maps showing the conformational space sampled by the minor species ensemble for CaM–4Ca²⁺. The minor state atomic probability maps are derived from PRE-driven simulated annealing calculations using an eight-member ensemble with a population of 10%, and plotted at multiple contour levels ranging from 0·1 (transparent blue) to 0·5 (opaque red). The gray probability density maps, plotted at a single contour level of 0·1 of maximum, show the conformational space consistent with interdomain PRE values ≤2 s⁻¹ and represent the major state ensemble characterized by no interdomain contacts and an occupancy of ∼90%. In the left-hand panel, all ensemble members are best fitted to the N-terminal domain (dark green) and the probability density maps are shown for the C-terminal domain. In the right-hand panel, all ensembles are best-fitted to the C-terminal domain (dark green) and the probability density maps are shown for the N-terminal domain. Adapted from Anthis et al. (Anthis & Clore, 2013; Anthis et al. 2011).

Fig. 10.

Pulse sequence for the 2D ¹⁵N–DEST experiment. Full details are given in Fawzi et al. (Fawzi et al. 2011b). During saturation experiments, the ¹⁵N CW saturation field is applied at a range of offset frequencies and at two different RF field strengths. During this period, a 180° ¹H pulse train is applied (with 100 ms spacing between pulses) in order to eliminate longitudinal cross-correlated relaxation interference between the ¹⁵N–¹H dipolar interaction and the ¹⁵N chemical shift anisotropy. Thus, for a saturation time of 0·9 s, for example, the saturation block would be repeated a total of n = 9 times. The optimal time for application of ¹⁵N saturation is the ¹⁵N–T₁ longitudinal relaxation time. In the reference experiment, the ¹⁵N saturation pulse is turned off (but the 180° ¹H pulse train is still applied).

Fig. 11.

Characterizing the exchange of Aβ peptides on the surface of large macromolecular assemblies by 15N–DEST and ¹⁵N lifetime line broadening (R_llb). (a) Pseudo-two-state kinetic scheme for exchange of Aβ monomers with the surface of amyloid protofibrils. The ‘dark’ state comprises an ensemble of states where each residue can either be tethered or in direct contact with the surface of the oligomer. (b) ¹⁵N–DEST profiles for Glu3 and Leu17 at two different RF fields (170 Hz, orange; 350 Hz, blue). Experimental data are shown as circles, and lines represent the best fit for the simple two-state model (dashed) and the tethered/direct contact model (solid). (c) Residue-by-residue characterization of Aβ in exchange with the protofibril surface. The top panel shows ¹⁵N–R_llb, with experimental data shown as black filled-in circles and calculated data shown as open circles for the simple two-state model (gray) or the tethered/direct contact model (blue). Also shown are profiles for the residue-specific partition coefficient 𝓀₃ (given by the ratio of direct-contact to tethered states) and ¹⁵N–R₂ values for the dark tethered states derived from the fits to the experimental R_llb and DEST data. Data are shown for Aβ(1–40) (blue) and Aβ(1–42) (red). (d) Kinetic scheme for binding of Aβ(1–40) to GroEL. Values are listed for the populations of free (p_A) and GroEL-bound (p_B) Aβ in the presence of 20 μM (in subunits) GroEL.(e) 15N–DEST profiles for Glu3, Ala21, and Ile32 at two different RF fields (250 Hz, light; 500 Hz, dark). Experimental data are shown as circles, and lines represent the best fit from the simple two-state model. (f) Residue-by-residue characterization of Aβ in exchange with GroEL. The top panel shows 15N–R_llb for 50 μM Aβ in the presence of 20 (circles) and 40 (diamonds) μM (in subunits) GroEL at spectrometer frequencies of 600 (blue) and 900 (red) MHz. Data are also shown for a control sample at 600 MHz (green) containing 50 μM Aβ40, 2·9 μM acid-denatured Rubisco, and 20 μM GroEL. The bottom panel shows back-calculated ¹⁵N–R_llb values for GroEL-bound Aβ at 600 (blue) and 900 (red) MHz spectrometer frequencies. Adapted from Fawzi et al. (2011b) and Libich et al. (2013).