Securely measuring the overlap between private datasets with cryptosets
- PMID: 25714898
- PMCID: PMC4340911
- DOI: 10.1371/journal.pone.0117898
Securely measuring the overlap between private datasets with cryptosets
Abstract
Many scientific questions are best approached by sharing data--collected by different groups or across large collaborative networks--into a combined analysis. Unfortunately, some of the most interesting and powerful datasets--like health records, genetic data, and drug discovery data--cannot be freely shared because they contain sensitive information. In many situations, knowing if private datasets overlap determines if it is worthwhile to navigate the institutional, ethical, and legal barriers that govern access to sensitive, private data. We report the first method of publicly measuring the overlap between private datasets that is secure under a malicious model without relying on private protocols or message passing. This method uses a publicly shareable summary of a dataset's contents, its cryptoset, to estimate its overlap with other datasets. Cryptosets approach "information-theoretic" security, the strongest type of security possible in cryptography, which is not even crackable with infinite computing power. We empirically and theoretically assess both the accuracy of these estimates and the security of the approach, demonstrating that cryptosets are informative, with a stable accuracy, and secure.
Conflict of interest statement
Figures


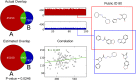
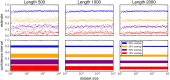
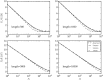
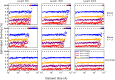

References
-
- Aggarwal CC, Yu PS (2008) A general survey of privacy-preserving data mining models and algorithms In: Aggarwal CC, Yu PS, Elmagarmid AK, editors, Privacy-Preserving Data Mining, Springer; US, volume 34 of Advances in Database Systems pp. 11–52. 10.1007/978-0-387-70992-5_2 - DOI
-
- Karakasidis A, Verykios VS (2011) Secure blocking+ secure matching = secure record linkage. J of Comp Science and Engineering 5: 101–106. 10.5626/JCSE.2011.5.3.223 - DOI
-
- Kuzu M, Kantarcioglu M, Durham E, Malin B (2011) A constraint satisfaction cryptanalysis of bloom filters in private record linkage In: Privacy Enhancing Technologies. Springer, pp. 226–245. 10.1007/978-3-642-22263-4_13 - DOI
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

